=> √10 = √(3 2 1) Construction 1 Take a line segment AO = 3 unit on the xaxis (consider 1 unit = 2cm) 2 Draw a perpendicular on O and draw a line OC = 1 unit 3 Now join AC with √10 4 Take A as center and AC as radius, draw an arc which cuts the xaxis at point E 5 The line segment AC represents √10 unitsThe point C shows the number √3 2 Represent √5 on the number line Solution Let us draw a number line, mark the center as point O and mark a point Q at number 2 such that it is 2cm from the center ie, l(OQ) = 2 units Now, draw a line QR perpendicular to the number line through the point Q such that l(QR) = 1 unit Draw seg ORThen, extend a line from 0 to the point you just plotted That line is the visual representation of the number 32i Some other properties are represented by the line on the Argand diagram The length of the line represents the modulus of the number √(3 2 2 2) = √13 The line also forms an angle with the positive side of the real axis
Representation Of Irrational Numbers On The Number Line 2 On Number Line
Represent 3 2/5 on the number line
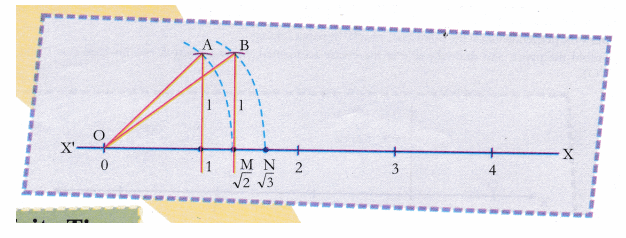
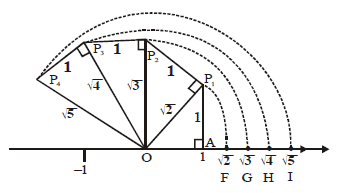
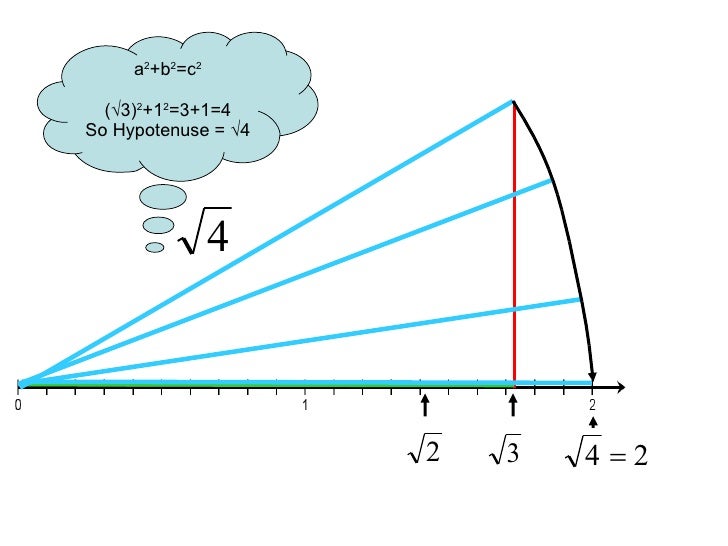
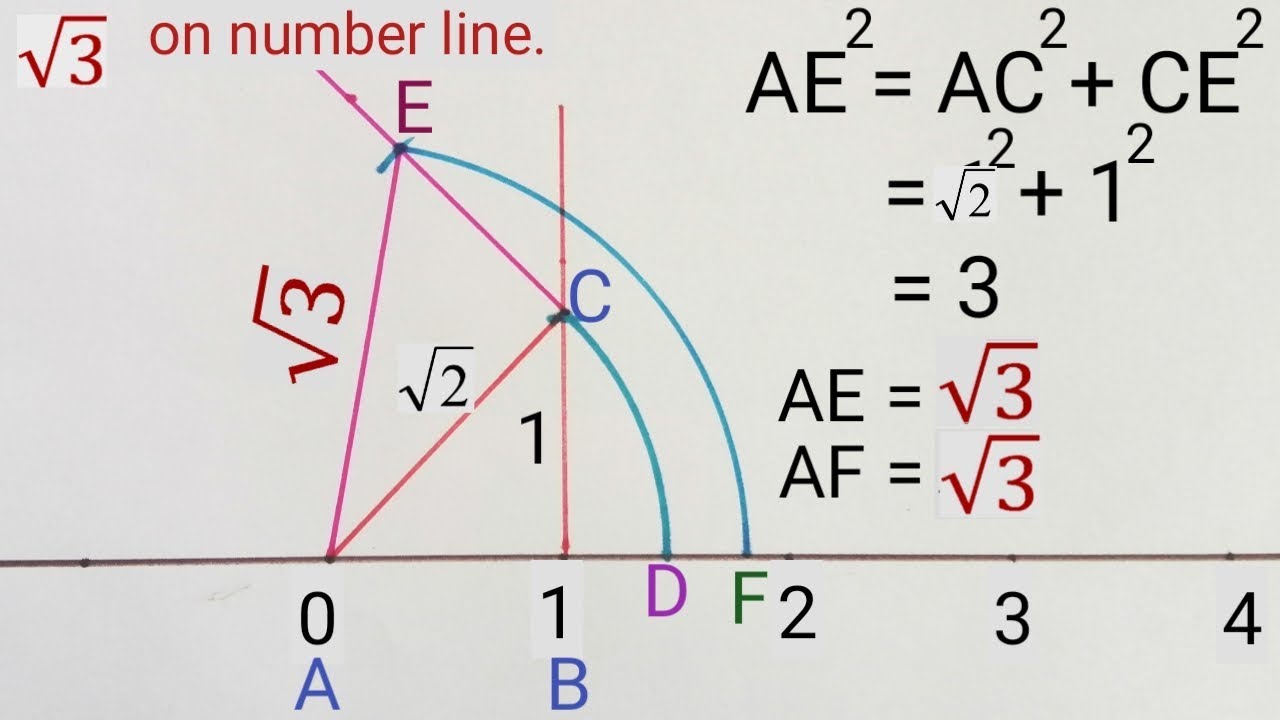
Represent 3 2/5 on the number line- √5 on the number line 5 can be written as the sum of the square of two natural numbers ie, 5 =1 4 =1 2 2 2 On the number line, Take OA = 2 units Perpendicular to OA, draw BA = 1 unit Join OB Using Pythagoras theorem, We have, OB= √5 Draw an arc with centre O and radius OB using a compass such that it intersects the number line Finding √2 On The Number Line 1 Finding √2,√3 and√4 on the number line An animated geometric construction 2 a 2 b 2 =c 2 1 2 1 2 =11=2 So Hypotenuse = √2 This line is 1 unit long 3 a 2 b 2 =c 2 ( √2) 2 1 2 =21=3 So Hypotenuse = √3 4 a 2 b 2 =c 2 ( √3) 2 1 2 =31=4 So Hypotenuse = √4 5



Locate Root 3 On The Number Line Represent Root 3 On Number Line Root 3 On Number Line Youtube
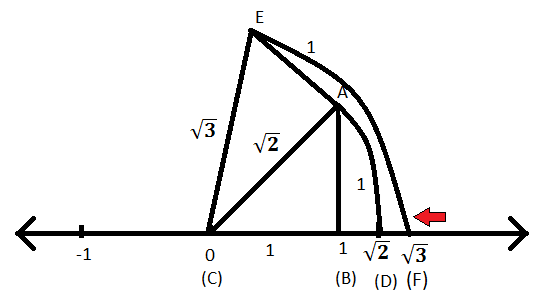
Now, to represent √32 on the number line Let us take the line BC as number line and point 'B' as zero, point 'C' as '1' and so on Draw an arc with centre B and radius BD, which intersects the number line at point 'E' Then, the point 'E' represents √32 Second method Construction method (fig2) Let A represent number 2, B represent 3 , on the number line Draw a segment BC perpendicular to segment AB & length same as AB (=1) Now ABC is a right angle triangle with sides AB & AC have unit lengths (Constructed) By Pythagoras theorem, diagonal AC length is sqrt (1^2 1^2)= sqrt 2 AC= sqrt 2Exercise 15 Question 1 Classify the following numbers as rational or irrational Solution (i) Since, it is a difference of a rational and an irrational number ∴ 2 – √5 is an irrational number (ii) 3 – = 3 – = 3 which is a rational number (iii) Since, = = , which is a rational number
=> √10 = √(3 2 1) Construction 1 Take a line segment AO = 3 unit on the xaxis (consider 1 unit = 2cm) 2 Draw a perpendicular on O and draw a line OC = 1 unit 3 Now join AC with √10 4 Take A as center and AC as radius, draw an arc which cuts the xaxis at point E 5 The line segment AC represents √10 units => √12 = √{32 (√3)2 } So, for representing √12 on number line, first we have to represent √3 on number line Now, √3 = √(2 1) => √3 = √{(√2)2 12 }The value √ 3 2 ≈ 0866 is greater than the value 1 2 = 05 For t = π 6, the xcoordinate is greater than the ycoordinate Therefore, x must be √ 3 2For t = π 3, the xcoordinate is less than the ycoordinate Therefore, x must be 1 2For special points in Quadrants II, III, and IV, use the values 1 2, √ 3 2, ∧ √ 2 2 with
This is easy Transfer Fig 16 onto the number line making sure that the vertex O coincides with zero (see Fig 17) We have just seen that OB = √2 Using a compass with centre O and radius OB, draw an arc intersecting the number line at the point P Then P corresponds to √2 on the number line (3 √3) 2 is a rational number (b) (5 – √5) 2 = (5) 2 (√5) 2 – 2×5×√5 On further calculation, we get, = 25 5 – 10√5 = 30 – 10√5 which is a irrational number Therefore, (5 – √5) 2 is an irrational number Represent the number √7 on the number line Answer d = 12/√(3^24^2) = 12/5 = 24 The other way is to realize that the shortest distance from a point to a line is along the line through the point and perpendicular to the given line Since our line has slope 4/3, the perpendicular line has slope 3/4 SO, the normal line is y = 3/4 x The two lines intersect where3/4 x = (4x12)/3




Rd Sharma Class 9 Chapter 1 Number System Free Pdf




Representation Of Irrational Numbers On The Number Line 2 On Number Line
1 Irrational Numbers on the Number Line Where are the points on the number line that correspond to the irrational numbers?SOLUTION Solution A, B, C, and D The product of two irrational numbers will be either a rational or an irrational number Consider the following example (√3√2)×(√3−√2)= 1 Both (√3√2) and (√3−√2) are irrational numbers and their product is 1 1 is an integer and since, all integers are rational numbers as well, weWrite 5 rational numbers between 5 & 6 7 Write 4 irrational numbers between √ & √ 8 Show that 1 ⃐ can be in the form (rational number) 9 √Is an irrational number Give reason 10 Represent on a number line √(a) 2 √(b) √5 (c) 10 11 Represent 4735 using successive magnification 12



Number System In Maths Geeksforgeeks



How To Draw 3 Root 2 On Number Line Mathematics Topperlearning Com G09h7see
For each pair of numbers, write two expressions to represent the distance between the numbers on a number line, then determine this distance a) b) 2 Arrange in order from least to greatest a) b) 5 8, √ 72 50, 2 √ 1 16, √ 9 5 3 √ 6, √ 24, 2 √ 6, √ 96 22 1 75 and 375 3 8 and 3 1 4 21 Each radical has index 2Write eachAnswer From the definition of the Argand diagram, we know that the complex number 𝑧 = 𝑎 𝑏 𝑖 will be represented by a point with Cartesian coordinates ( 𝑎, 𝑏) Hence, 𝑍 will be represented by the point 𝐴 ( 8, 1) In our next example, we will identify complex numbers and Ans i) Irrational numbers are √2, √3, √5, √3 etc, which can be shown in real number line therefore every irrational number is a real number ii) All positive numbers as an ex √1, √2, √3, √4 can be represented on the number line but the square root of a negative number, √ (–m ) does not existso it is false




Represent Root 2 Root 3 Root 5 Root 6 On Number Line Brainly In




Ask Questions For Cbse Class 9 Maths Number Systems
Q5 Show that 3√5 is an irrational number Ans Let us assume 3√5 is a rational number, 3√5 = p/q, where p and q are coprimes, √5 = p/3q Clearly √5 is irrational, while number on right q ≠ 0 are rational ∴ Irrational = Rational But above deduced can't be right Therefore our supposition is wrong making 3√5 an irrational number Which number line represents the solution set for the inequality x 24?Using Pythagoras theorem We can write the √10 as below √10 = (√91) This can be written as √10 = (√3 2 1 2) The construction steps are shown below Take a line segment AO = 3 units on x axis Here consider 1 unit = 2 cm Draw a perpendicular on O, name it as OC such that OC = 1 unit




6 X 5 Number Line Novocom Top



Represent 3 5 9 4 10 5 On The Real Number Line Sarthaks Econnect Largest Online Education Community
2 √3 = 2 √3 Rational Number Irrational Number = Irrational Number Eg 7 √3 = 7 √3 Non 0 Rational Number / Irrational Number = Irrational Number 3 / √3 = √3 Class 9 Exercise 11 Number System (Multiple Choice Questions) Write the correct answer in each of the following Q1 Every rational number is A) a natural number B) an integer C) a real number D) a whole number Q8 A rational number between √ 2 and √ 3 is;√32(B) Describe the mathematical relationships found in the base10 place value system through the hundred thousands place √34(I) Determine if a number is even or odd using divisibility rules Processing Standards √31(A) Apply mathematics to problems arising in




Locate 3 On Number Line Maths Questions




Represent 3 On Number Line Brainly In
How do we represent √2 on the number line?You have to represent 2√(3) in number line So first mark 2 in number line and then from 2 use geometric compass and make a circle with the same length of √(3) as radious in number line So between 1 and 2 where the circle cuts that is 2√(3) and between 2 and 3 where tPLOT COMPLEX NUMBERS IN THE COMPLEX PLANE A real number can be represented as a point on the real number line Since a complex number a bi has two parts, = √ (3) 2 − 4) 2 = √ 25 = 5 b z of the point (a,b) in the rectangular coordinate system formed by the complex plane For a and b not both zero, let r represent the length of
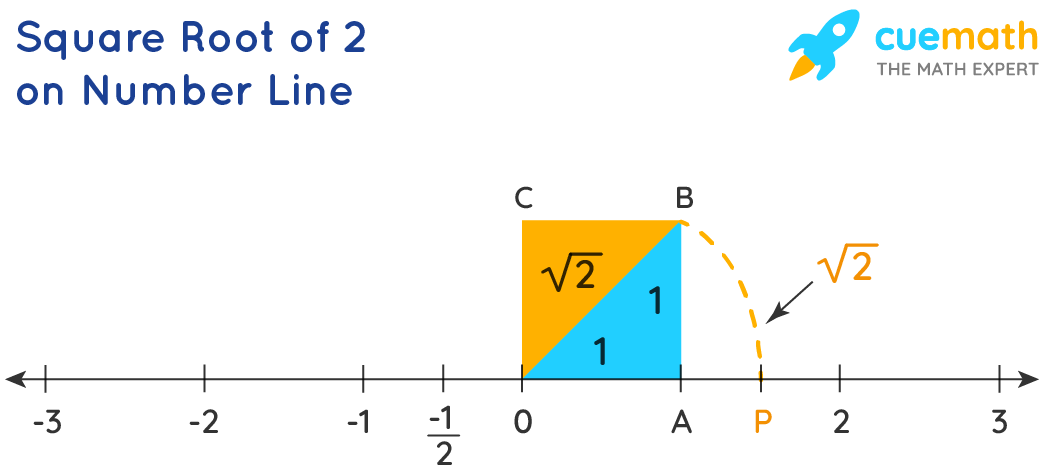



Square Root Of 2 How To Find The Square Root Of 2 Cuemath




How Can We Represent 2 On A Number Line Quora
Pets & Animals Represent root 23 on the number line, Locate root 23 on number line, √23 on the number line, 1) Represent √2 (root 2) on number line https//youtube/tbulE993EfM 2) Represent √3 (root 3) on the number line https//youtube/SuKSbqkYRbk 3) Represent √5 (root 5) on the number lineWrite the following rational numbers in decimal form and state which type of decimal expansion it is a) 3 b) 3 marks questions Q14 Represent √32 on the number line Q15 2If a = −√ and b = , then find a2 – b Q16 Rationalize the denominator a) √ − b) √ Q17 Simplify and find the value of 3 The value of (2√3 )( 2√3 ) is (i)1 (ii)1 (iii) 2 (iv) none of these 4 (27)2/3 is equal to _____ (i) 9 (ii) 1/9 (iii) 3 (iv) none of these 5 Simplify 3 √2 x 4 √ 3 6 Find the two rational numbers between ½ and 1/3 7 Find two irrational numbers between 2 and 3 8 Multiply √5 by 6 √2 9 Express 0 in the form p




Ncert Class 9 Maths Lab Manual Construct A Square Root Spiral Cbse Tuts




Locate 10 On Number Line Maths Questions
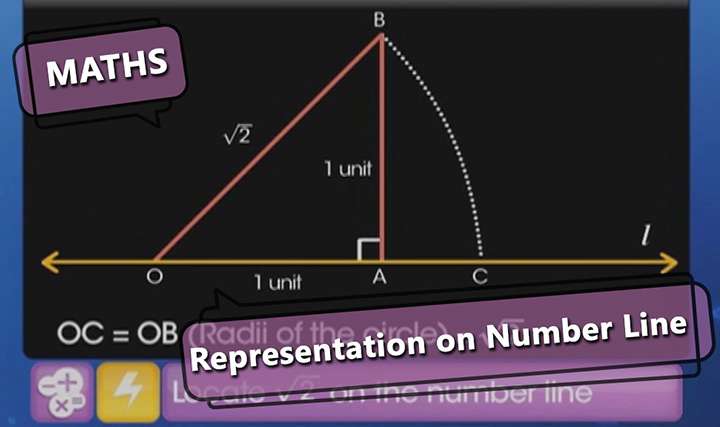
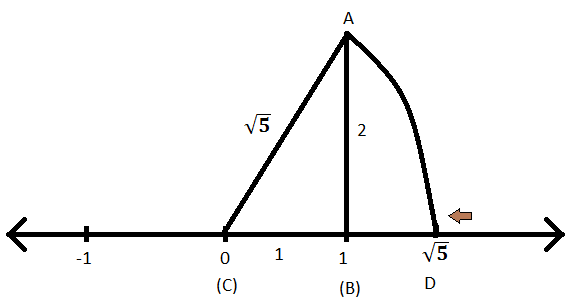
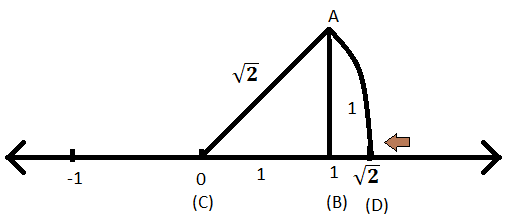
Represent the numbers √5 and √10 on a number line 03 and 05 Write any three rational numbers between the two numbers given below 23 and 233 Write any three rational numbers between the two numbers given belowWhich are the solutions of the quadratic equation? OD = √2 But √2 is not a rational number as it cannot be expressed in the form p/q From this we infer that there are points on the number line which are not rational If we express √2 in the decimal form, we observe that it does not terminate and is nonrecurring Such numbers are called irrational numbers



How Do We Represent 2 3 On A Number Line Quora




Irrational Number Wikipedia
Locate √5, √10 and √17 on the number line Solution √5 on the number line 5 can be written as the sum of the square of two natural numbers ie, 5 =1 4 =1 2 2 On the number line, Take OA = 2 units Perpendicular to OA, draw BA = 1 unit Join OB Using Pythagoras theorem, We have, OB= √5 Draw an arc with centre O and radius OBA Complex Number is a combination of a Real Number and an Imaginary Number A Real Number is the type of number we use every day Examples 1238, ½, 0, −00 When we square a Real Number we get a positive (or zero) result 22 = 2 × 2 = 4 12 = 1 × 1 = 1 02 = 0 × 0 = 0 What can we square to get −1?Represent √32 geometrically on the number line Report Posted by Riya Singh 3 years, 2 months ago CBSE > Class 09 > Mathematics 1 answers Prashant Chaudhary 3 years, 2 months ago




Number Line Definition Operation Uses Dewwool



Represent 3 5 9 4 10 5 On The Real Number Line Sarthaks Econnect Largest Online Education Community
👍 Correct answer to the question Which point on the number line best represents the approximate value of 23?X = 7 and x = 1 The area of a rectangular room is 750 square feet The width of the room is 5 feet less than the length of the room Which equations can be used to solve for y, the length of the room?Answers 1 Answer Mathematics, 2130 If value of cos330° is √3/2 then find tan165° Answers 1 Answer You know the right answer?



How Do We Represent 3 On Number Line Quora




Represent The Numbers Sqrt 5 And Sqrt 10 On A Number Line Algebra Shaalaa Com
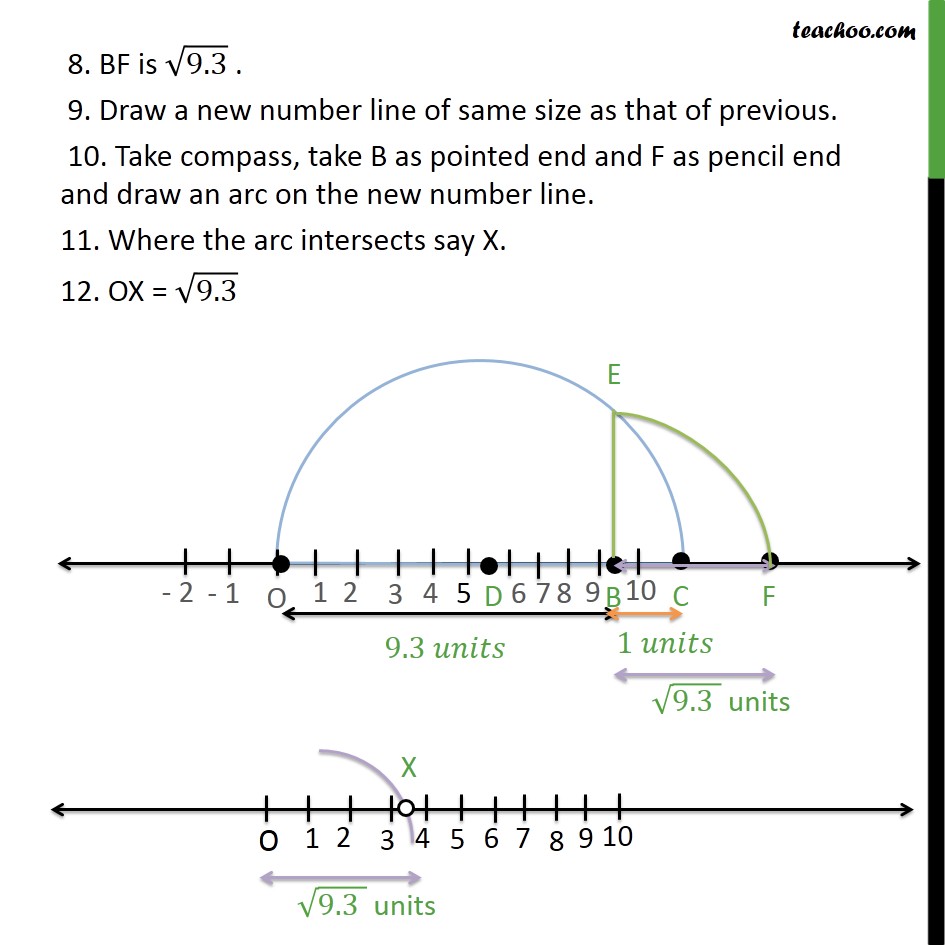
An irrational number √2 is represented on the number line Learning Outcome Students can represent any irrational number on number line by using above method eg, (√3) 2 = (√2) 2 (1) 2 At M, by paper folding draw perpendicular BM on the number line of 1 unit Join OB With O as centre and OB as radius draw an arc intersecting the line at N Thus OB = ON = √3 on the number lineAnswers 3 Answer Mathematics, If sin(x) = 0 and cos(x) = 1, what is tan(x)? Draw a line AB = 93 units on number line Extend B to C such that BC = 1 unit Find the midpoint AC say point D and draw a circle on OC Draw a perpendicular to line AC passing through point B Let it intersect the circle at F Taking B as centre and BF as radius, draw an arc intersecting number line at G BF is √(93)




How To Locate Root 3 On A Number Line Spiral Method Mathematics Topperlearning Com Y0wmee



Rational Numbers On The Number Line
A) (√ 2 √ 3)/2Lesson Worksheet Solving Linear Equations over the Real Numbers Mathematics Start Practising In this worksheet, we will practice solving linear equations over the real numbers and representing their solutions on a number lineX^2 = 9x 6 9 √105/2, 9 √105/2 What are the solutions to x^2 8x 7 = 0?



Cbse Class 9 Maths Lab Manual An Irrational Number Cbse Sample Papers
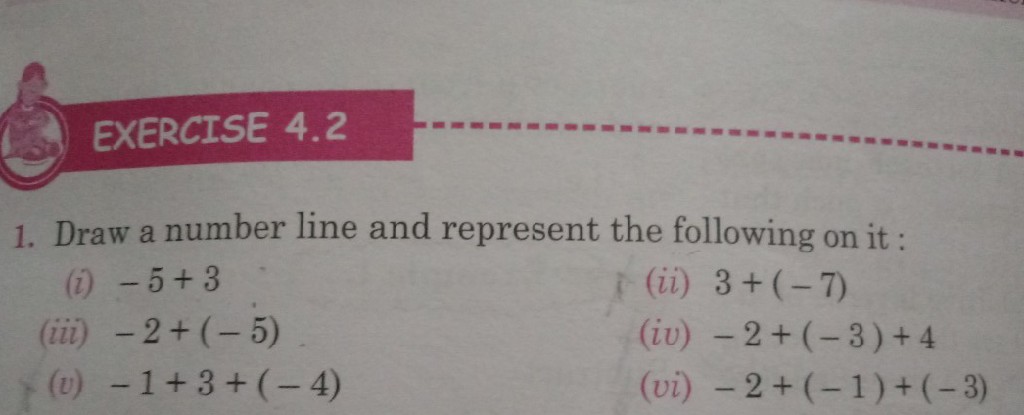



Exercise 4 2 1 Draw A Number Line And Represent The Followi Scholr
When written with a rational denominator, the expression 2√3/3√2 can be simplified as (1) √2/3 (2) √3/2 (3) √6/3 (4) 2/3 asked in Real Numbers by nchi ( 4k points) real numbersRepresents √5 on the number line Ex 12 Class 9 Maths Question 4 Take a large sheet of paper and construct the 'square root spiral' in the following fashion Start with a point O and draw a line segment OP 1, of unit lengths Draw a line segment P 1, P 2 As we know irrational number divided by a rational number results in an irrational number Question 4 Represent \(\sqrt{93}\) on the number line Solution To represent \(\sqrt{93}\) on the number line We mark a point B on the number line so that AB = 93 units Again mark a point C so that BC = 1 unit



Square Root Of 2 Wikipedia




Represent 2 Root 3 On Number Line Mathematics Topperlearning Com R3keaipp
As an example, let us locate √ 2 on the number line This is easy Remember that √ 2 is the length of the diagonal of the square whose side is 1 unit (How?)Simply construct a square and transfer the length of one of
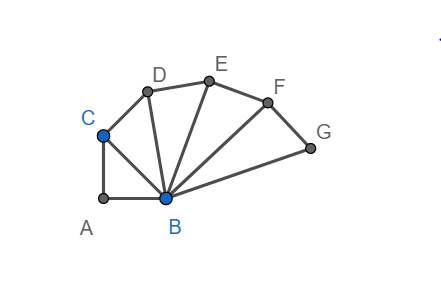



Represent Sqrt7 On The Number Line Class 10 Maths Cbse



Ex 1 5 4 Ex 1 5



Represent Square Root Of 7 5 On The Number Lin Gauthmath




Locate 2 On Number Line Maths Questions




Q3 Represent The Following Num Lido



How Do We Represent 2 3 On A Number Line Quora




Ncert Solutions For Class 9 Maths Chapter 1 Number Systems



How Do We Represent 3 On Number Line Quora
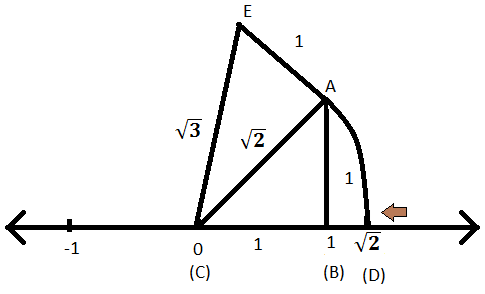



Representation Of Irrational Numbers On The Number Line 2 On Number Line



Number Lines Definition Representation 1 To 100 Examples




What Is A Real Number In Math Solved




How To Represent Root 2 On Number Line With Steps Brainly In
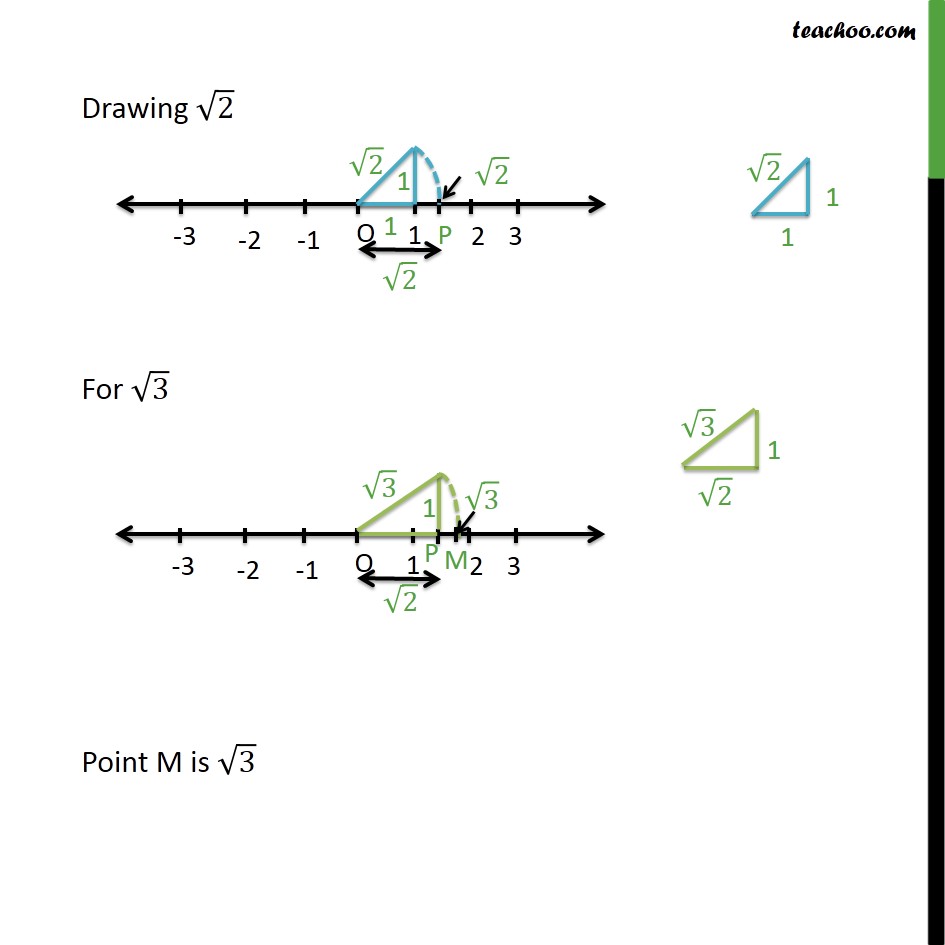



Represent Root 3 On The Number Line With Video Chapter 1 Class 9




Ncert Exemplar Class 9 Maths Chapter 1 Solutions Number System Download Free Pdf



Eg4 Nic In Jnv Dfiles Ebooks Ir Numbersystem Pdf




Solve The Equation 3x 2 2x 3 And Represent The Solution On The Number Line




Represent 2 2 On The Number Line Youtube
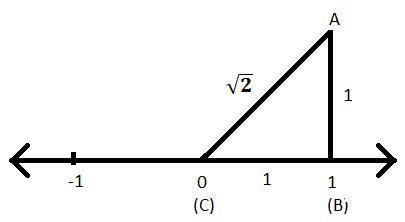



Representation Of Irrational Numbers On The Number Line 2 On Number Line




Draw The Number Line And Represent The Following Rational Numbers On It I 3 4 Ii 5 8 Iii 7 3 Iv 7 8




Ask Questions For Cbse Class 9 Maths Number Systems




How To Represent 8730 9 On Number Line Old Real Numbers Maths Class 9



How Do We Represent 3 On Number Line Quora
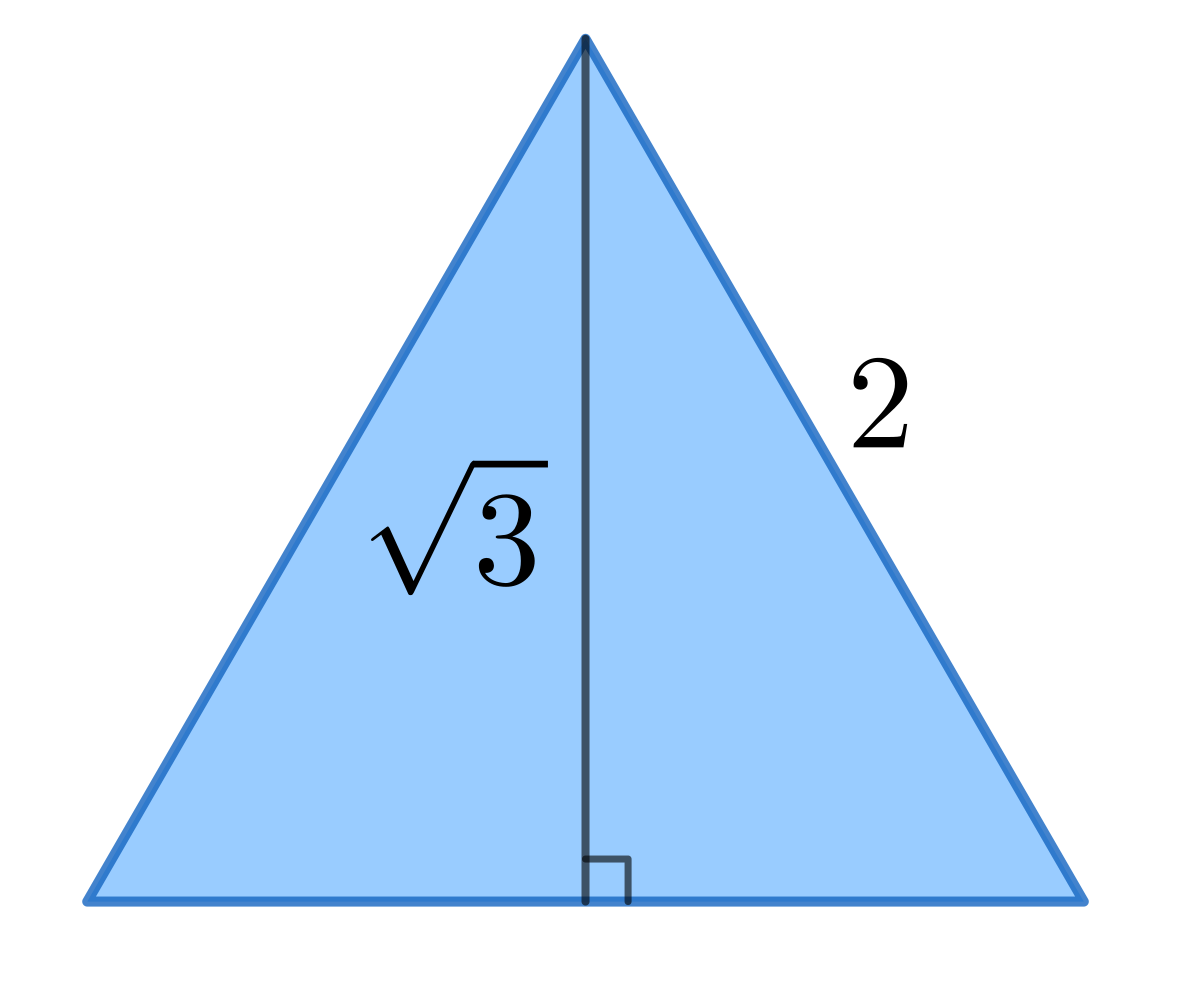



Square Root Of 3 Wikipedia




Ncert Class 9 Maths Lab Manual Construct A Square Root Spiral Cbse Tuts



Represent The Following Irrational Numbers On The Number Line I 3 Ii 4 7 Iii 6 5 Sarthaks Econnect Largest Online Education Community



Representation Of Irrational Numbers On The Number Line 2 On Number Line




Represent Root 2 Root 3 Root 5 And Root 6 On A Number Line Youtube




Cbse Class 9 Maths Lab Manual Square Root Spiral Cbse Sample Papers



1




Ncert Solutions For Class 9 Maths Chapter 1 Number Systems



Representing Real Numbers On Number Line And Law Of Exponents Class 9 Mathematics Class 9 Notes Edurev



Representation Of Irrational Numbers On The Number Line 2 On Number Line




Real Numbers Type Or Division Solved Example Problems Mathematics




Real Numbers Geeksforgeeks




How Do We Represent 2 3 On A Number Line Quora




Ask Questions For Cbse Class 9 Maths Number Systems




Locate Root 3 On The Number Line Represent Root 3 On Number Line Root 3 On Number Line Youtube




Represent 2 Root 3 On A Number Line Maths Number Systems Meritnation Com




Represent Root 3 2 On The Number Line Locate Root 3 2 On Number Line 3 2 On Number Line Youtube




Represent 3 7 On Number Line Brainly In



Q Tbn And9gcq3dci71zygo5srkpm 1gchk9gizckeiw8n16f8dr 6i3fs936 Usqp Cau




Cbse Class 9 Maths Lab Manual Square Root Spiral Cbse Sample Papers



Finding 2 On The Number Line



Locate Root 3 On The Number Line Represent Root 3 On Number Line Root 3 On Number Line Youtube
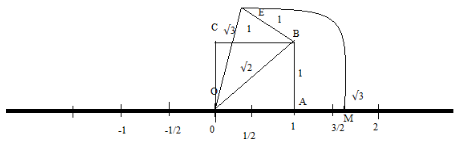



Represent Sqrt 3 On The Real Line Class 9 Maths Cbse
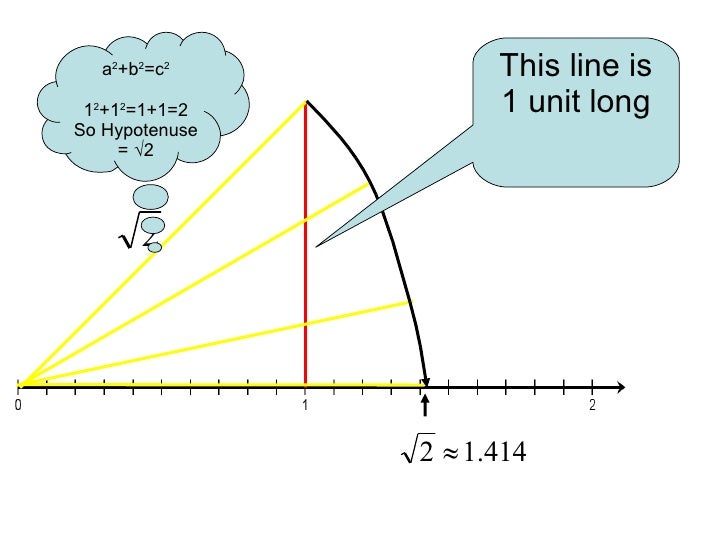



Finding 2 On The Number Line




Worked Example Whole Numbers On The Number Line Video Khan Academy




Representing Irrational Numbers 2 3 On The Number Line Part 3 Youtube




Cbse Ncert Solution For Class 9 Maths Number Systems




Represent 2 Root 3 On Number Line Mathematics Topperlearning Com R3keaipp




Represent 7 3 Using Number Line Maths Number Systems Meritnation Com




Represent 3 2 On Number Line Brainly In




Representing Real Numbers On Number Line And Law Of Exponents Class 9 Mathematics Class 9 Notes Edurev




How To Represent Root 2 And Root 3 On Number Line I Represent Irrational Number On Number Line Youtube




Represent Root 3 On The Number Line With Video Chapter 1 Class 9



Represent Sqrt7 On The Number Line Class 10 Maths Cbse




Represent 9 3 On The Number Line




Represent Root 2 On The Number Line With Video Teachoo



Represent 3 5 9 4 10 5 On The Real Number Line Sarthaks Econnect Largest Online Education Community



Representation Of Real Numbers On Number Line Steps Method Real Number Line Examples




Locate 2 On Number Line Maths Questions




Represent The Real Number Root 2 Root 3 Root 5 On A Single Number Line Brainly In



Represent 3 5 9 4 10 5 On The Real Number Line Sarthaks Econnect Largest Online Education Community




Ncert Solutions For Class 9 Maths Chapter 1 Number Systems



Q Tbn And9gcqyelewoszlg O1ndidwzu1b7g0lcrdagbpxs0nttrx5cedumj5 Usqp Cau




Ncert Solutions For Class 9 Maths Chapter 1 Number Systems



Q Tbn And9gcqpz05bsr6khqubbu3eptmf0ypov0wjgl92nitqgoukqz9u7fvo Usqp Cau




Ncert Exemplar Class 9 Maths Solutions Chapter 1 Number Systems Cbse Tuts
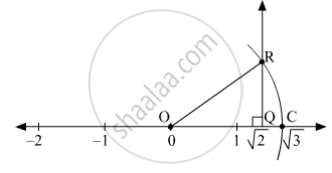



The Number 2 Is Shown On A Number Line Steps Are Given To Show 3 On The Number Line Using 2 Fill In The Boxes Properly And Complete The Activity Mathematics Shaalaa Com




Represent The Real Number Root 2 Root 3 Root 5 On A Single Number Line Brainly In
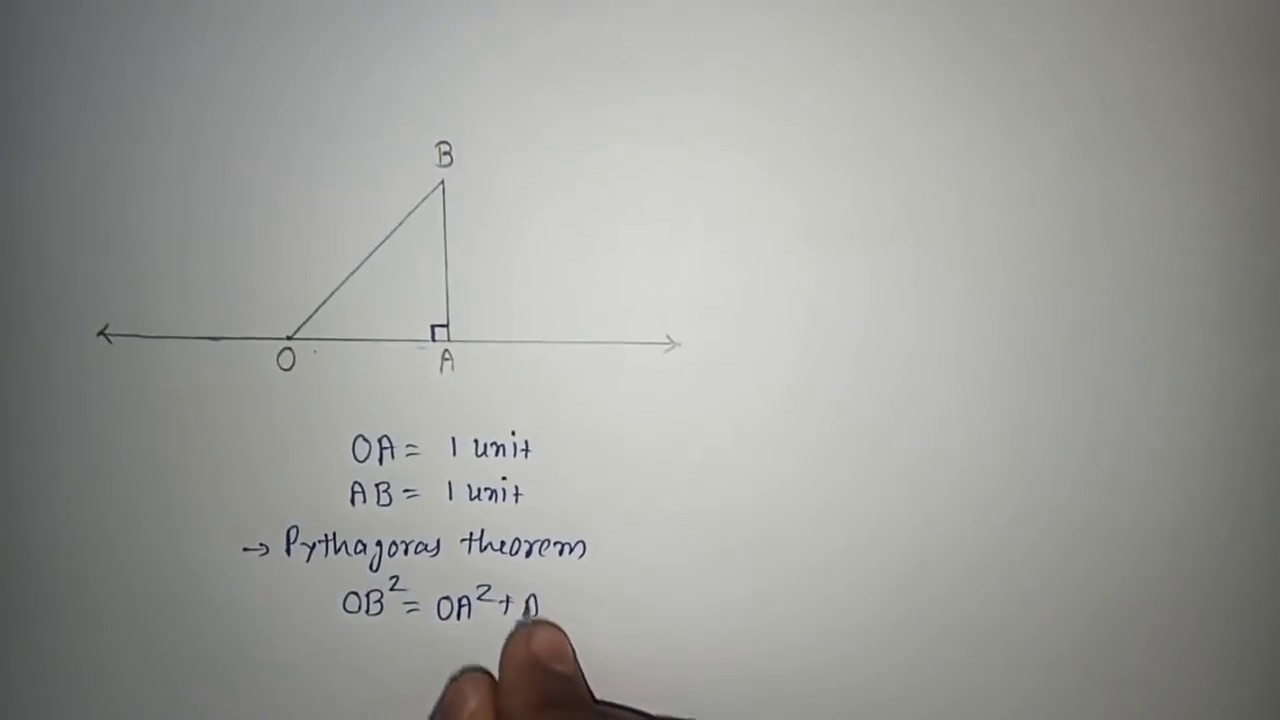



Represent Root 3 On Number Line Youtube



Square Root Of 2 Wikipedia
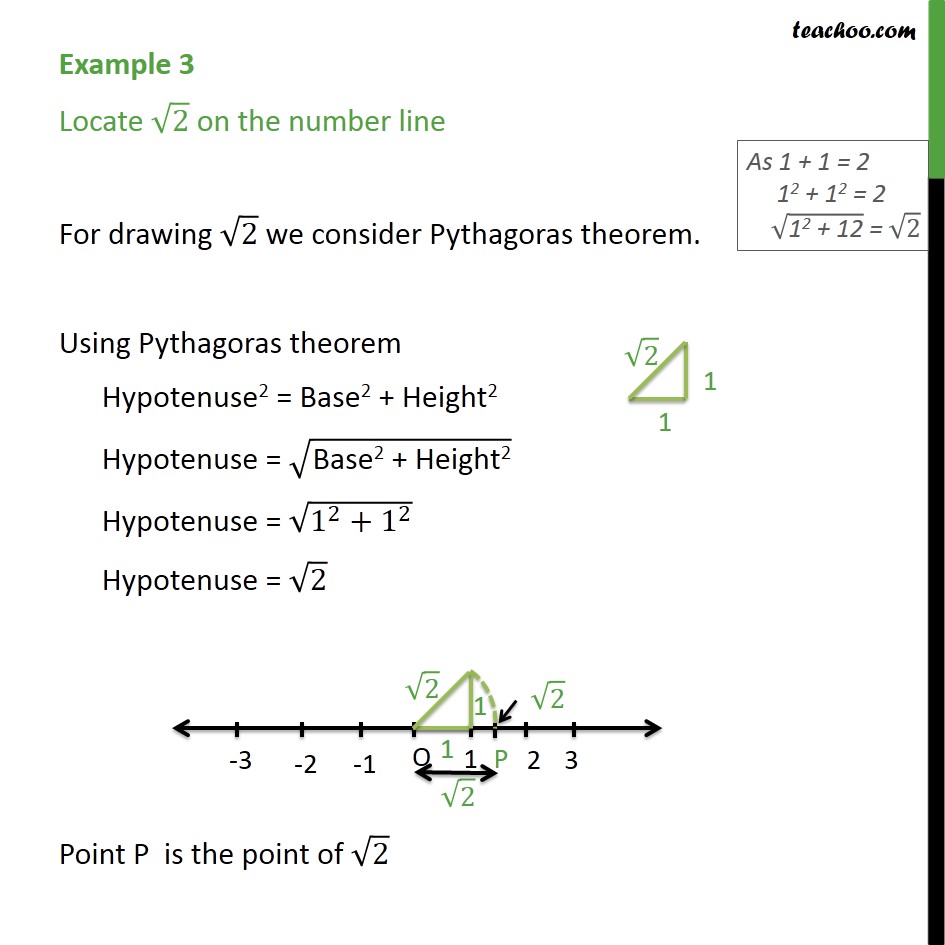



Represent Root 2 On The Number Line With Video Teachoo




Represent 9 3 On The Number Line



How Do We Represent 3 On Number Line Quora



Number Lines Definition Representation 1 To 100 Examples




Represent 7 On The Number Line




How To Draw 3 Root 2 On Number Line Mathematics Topperlearning Com G09h7see



0 件のコメント:
コメントを投稿