三角形とはどんな図形 辺の長さ 角度の定理や種類を知ろう 個別指導塾wam
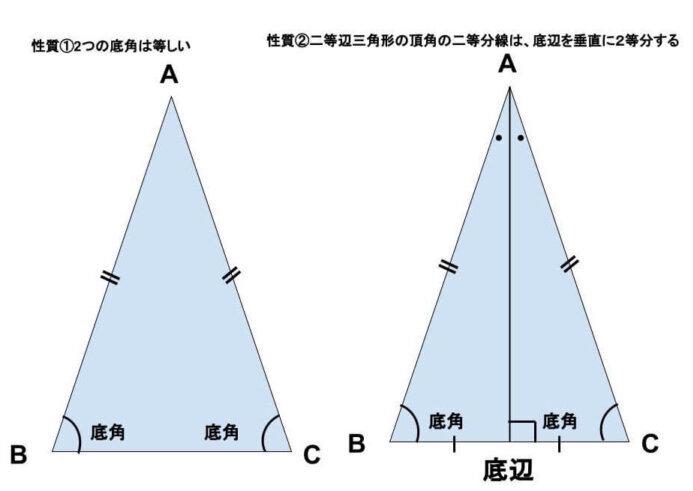
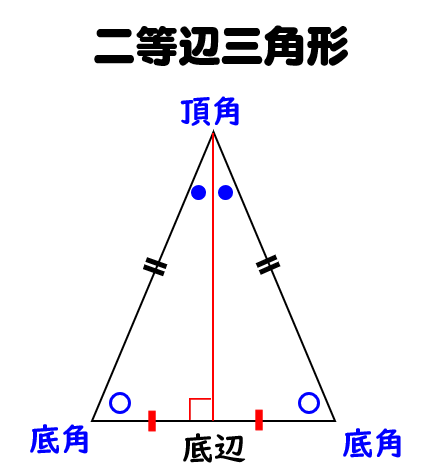
二等辺三角形の性質・定義と定理のポイントは！ 二等辺三角形とは2つの等しい辺を持つ三角形のこと 二等辺三角形の等しい辺で挟まれた角を頂角、残り2つの角を底角という Show more二等辺三角形 （にとうへんさんかくけい、 英 isosceles triangle ）は、 三角形 の一種で、3 本の 辺 のうち（少なくとも）2 本の辺の長さが等しい 図形 である。 長さの等しい 2 辺を 等辺 といい、
三角形 辺の長さ 求め方 二等辺三角形
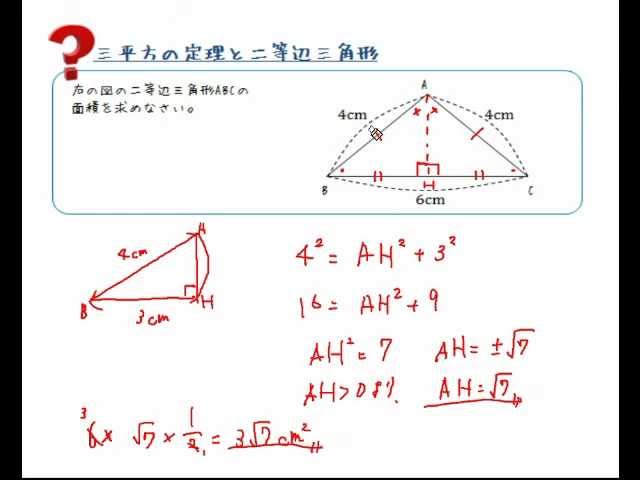
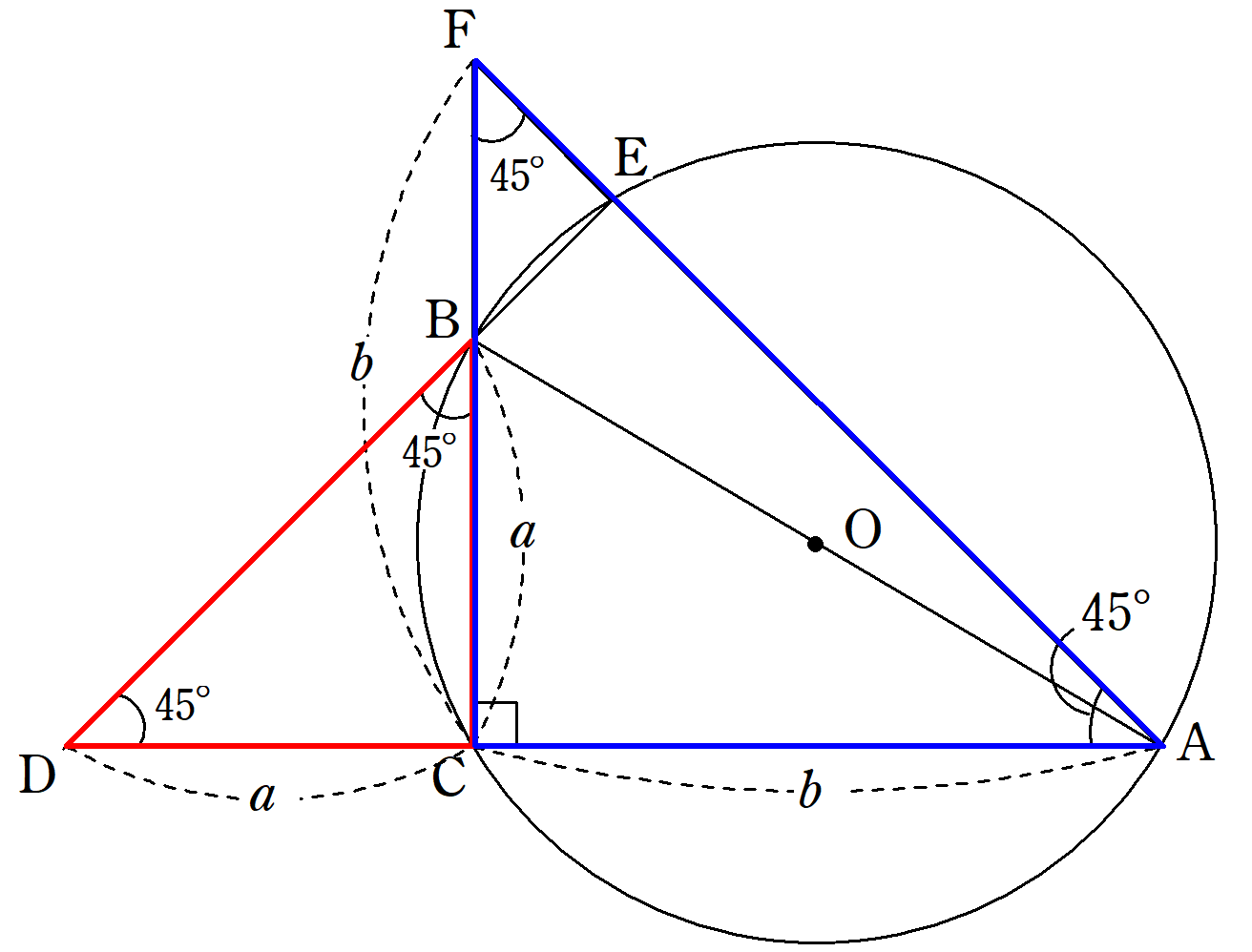
三角形 辺の長さ 求め方 二等辺三角形-中線定理とは 中線定理 とは，三角形の辺の長さに関する以下の定理のことです．エジプトの数学者パップスにちなんで，パップスの定理と呼ぶこともあります． 中線定理 ABC A B C において，辺直角二等辺三角形の辺の比は「三平方の定理」から導くことができます。 直角二等辺三角形の底辺と高さの長さは同じです。 底辺（高さ）の長さを「1」として、三平方の定理に代入すると「斜辺 2
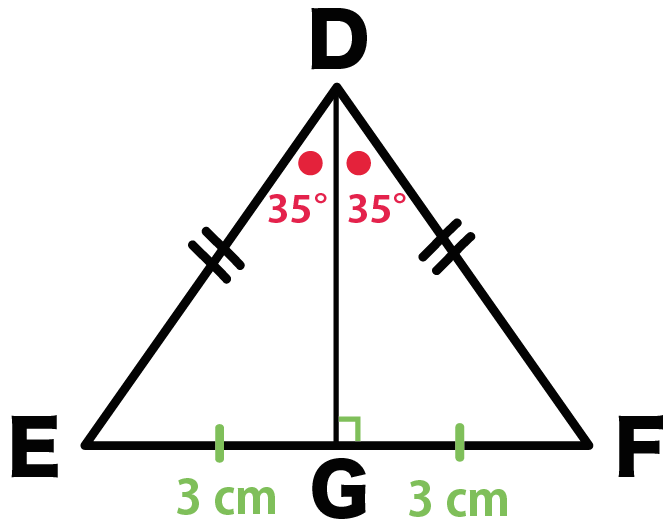
3分でわかる 二等辺三角形の2つの定理 性質 Qikeru 学びを楽しくわかりやすく
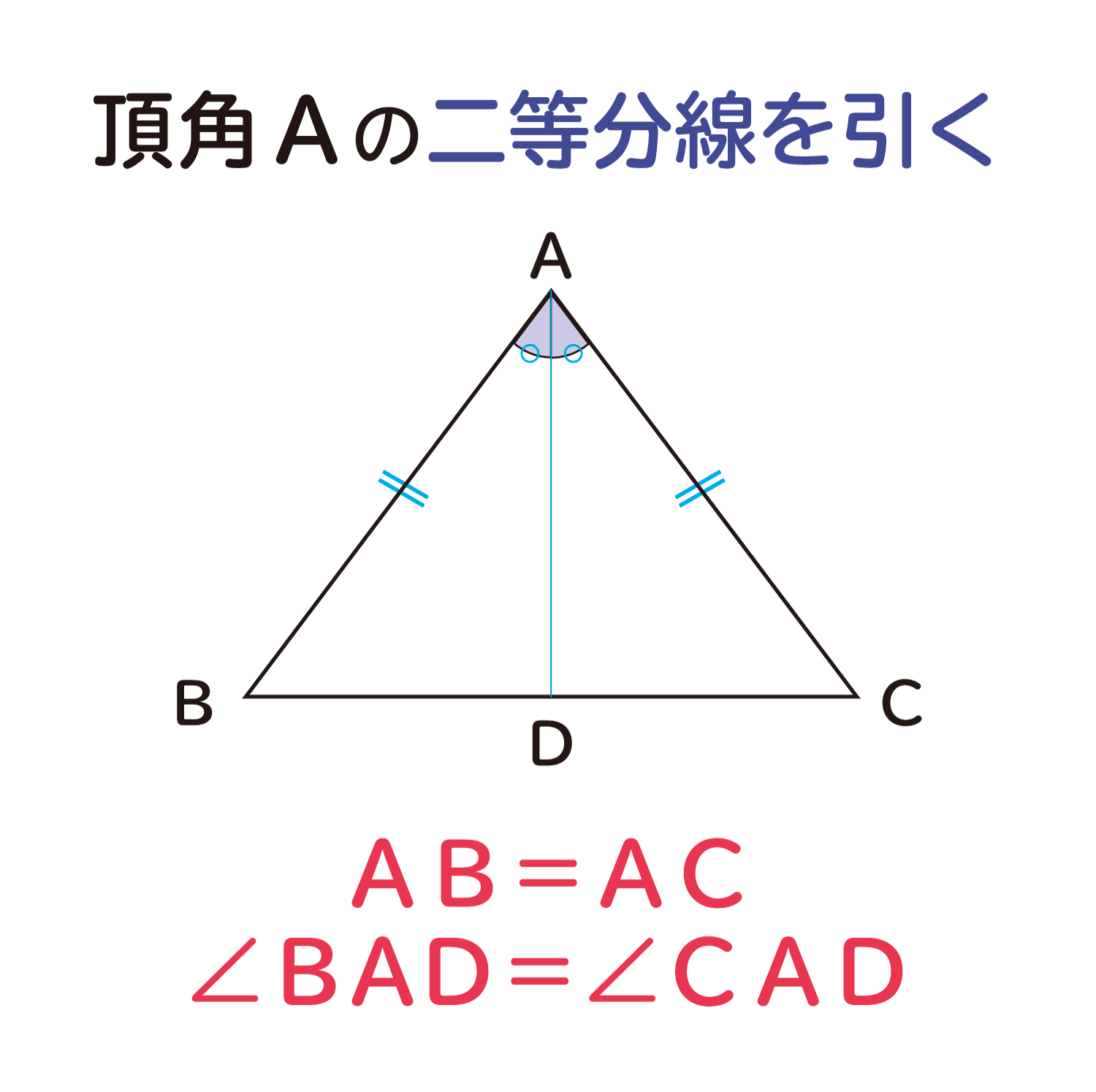
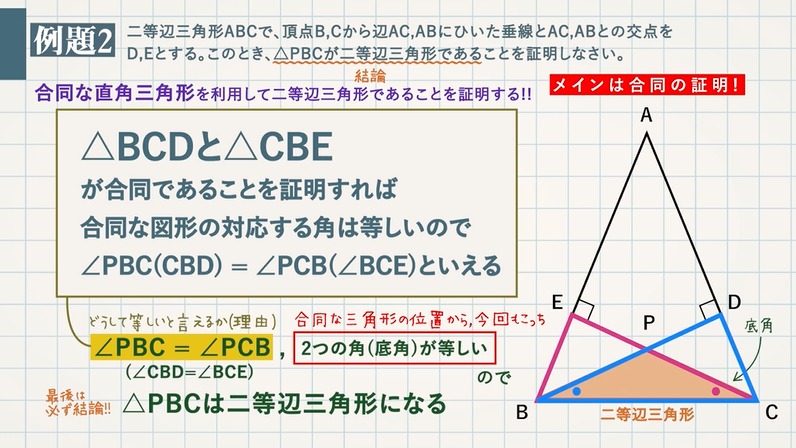
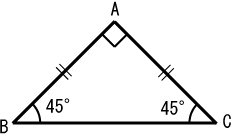
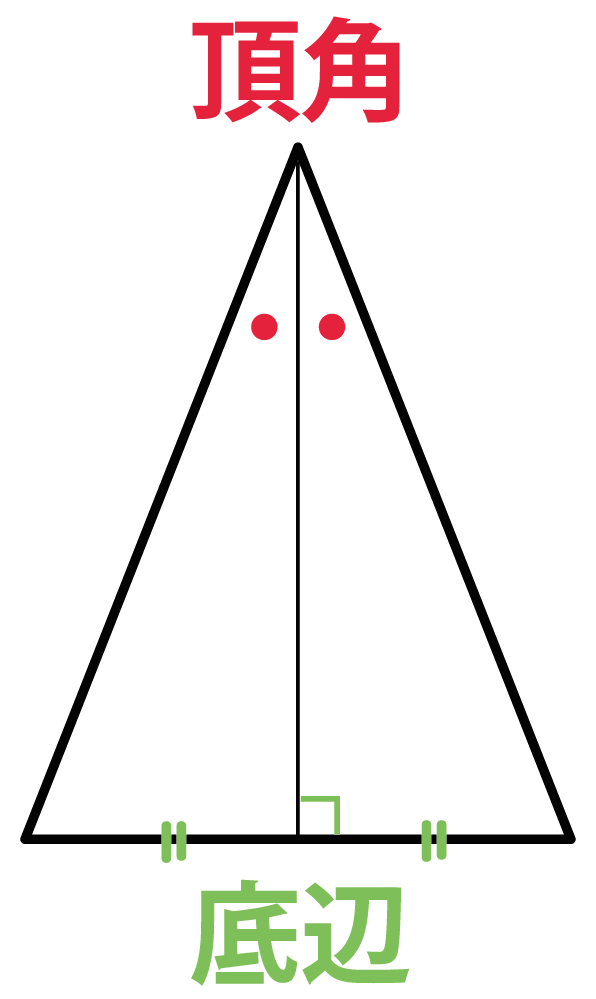
分からないので教えてください🙏 写真の問題で なぜ三角形PCHが直角二等辺三角形になるんですか？ 直角なのは分かりますが、二等辺三角形なのが分からなくて💦 お願いしますm(_ _)m 二等辺三角形の定理 定理 二等辺三角形の性質 二等辺三角形の2つの底角は等しい。 二等辺三角形の頂角の二等分線 二等辺三角形の頂角の二等分線は，底辺を垂直に2等分する。二等辺三角形になるための条件を考察することができる。 定理の逆について理解することができる。 問題 右の図で， ABCは んな三角形だろうか？ 4 B 二等辺三角形になるため の条件を見いだ
直角二等辺三角形（ちょっかくにとうへんさんかくけい、英 isosceles right triangle ）は、二等辺三角形の持つ特徴に加え、直角三角形の持つ特徴を併せ持つ図形である。 3つの角のうち2つの角が二等辺三角形の底角が等しいことの証明 AB=ACの二等辺三角形ABCで∠ABC=∠ACBを証明する。 A B C 証明 A B C D 頂角BACの二等分線をひき、底辺BCとの交点をDとする。 ABDと ACDにおい 直角二等辺三角形の定義 つの角のうち、 つの角がそれぞれ である三角形を「直角二等辺三角形」という。 残りの頂角は 、直角ということですね。 定理「辺の長さの比が 」 直角二等
三角形 辺の長さ 求め方 二等辺三角形のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 中点連結定理 Mn Mn 1 2bc 教遊者 | 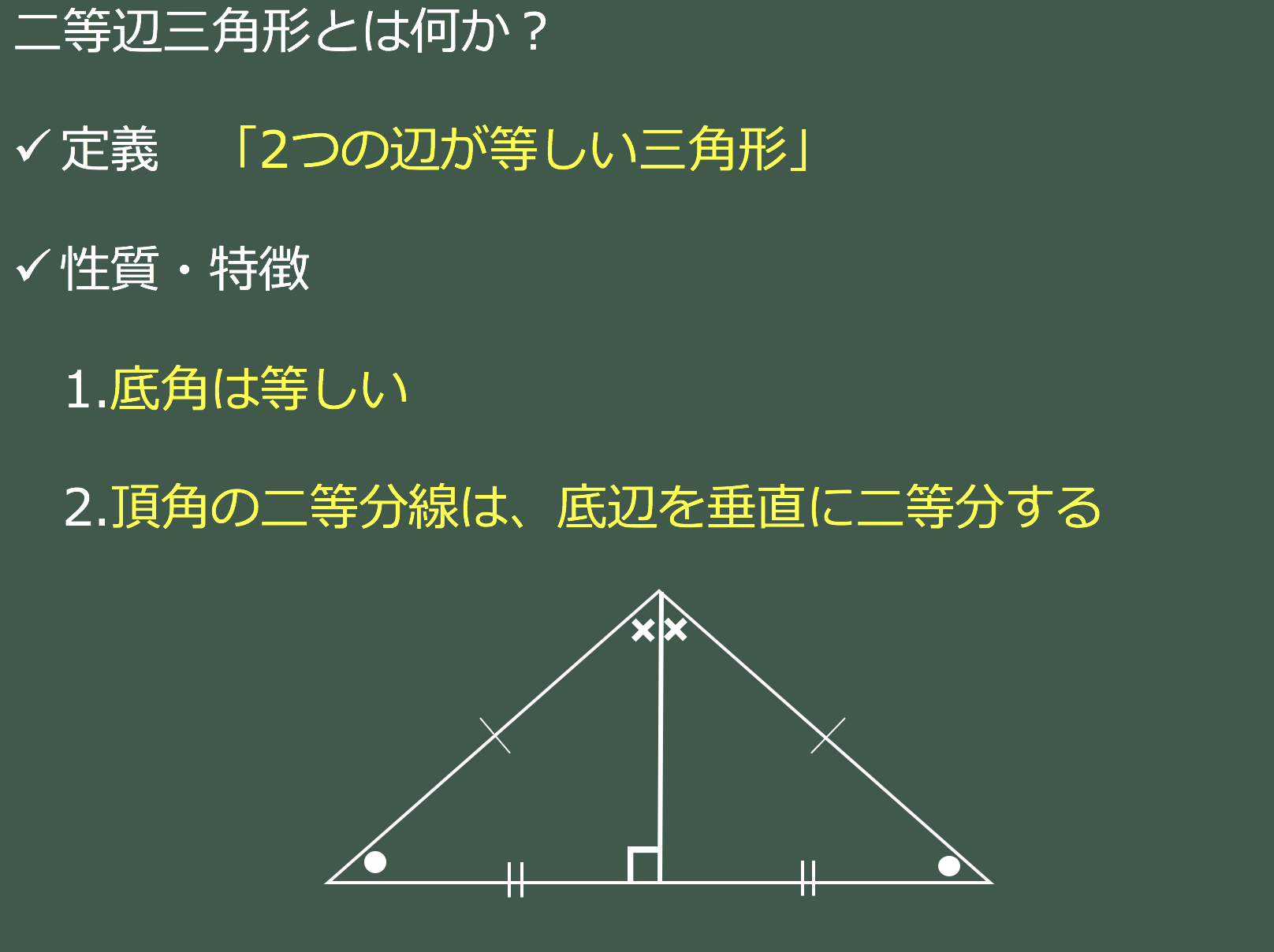 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
「三角形 辺の長さ 求め方 二等辺三角形」の画像ギャラリー、詳細は各画像をクリックしてください。
 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
「三角形 辺の長さ 求め方 二等辺三角形」の画像ギャラリー、詳細は各画像をクリックしてください。
 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
「三角形 辺の長さ 求め方 二等辺三角形」の画像ギャラリー、詳細は各画像をクリックしてください。
 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
「三角形 辺の長さ 求め方 二等辺三角形」の画像ギャラリー、詳細は各画像をクリックしてください。
 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
「三角形 辺の長さ 求め方 二等辺三角形」の画像ギャラリー、詳細は各画像をクリックしてください。
 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
「三角形 辺の長さ 求め方 二等辺三角形」の画像ギャラリー、詳細は各画像をクリックしてください。
 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
「三角形 辺の長さ 求め方 二等辺三角形」の画像ギャラリー、詳細は各画像をクリックしてください。
 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
「三角形 辺の長さ 求め方 二等辺三角形」の画像ギャラリー、詳細は各画像をクリックしてください。
 中点連結定理 Mn Mn 1 2bc 教遊者 | 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
「三角形 辺の長さ 求め方 二等辺三角形」の画像ギャラリー、詳細は各画像をクリックしてください。
中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 | 中点連結定理 Mn Mn 1 2bc 教遊者 |
「三角形 辺の長さ 求め方 二等辺三角形」の画像ギャラリー、詳細は各画像をクリックしてください。
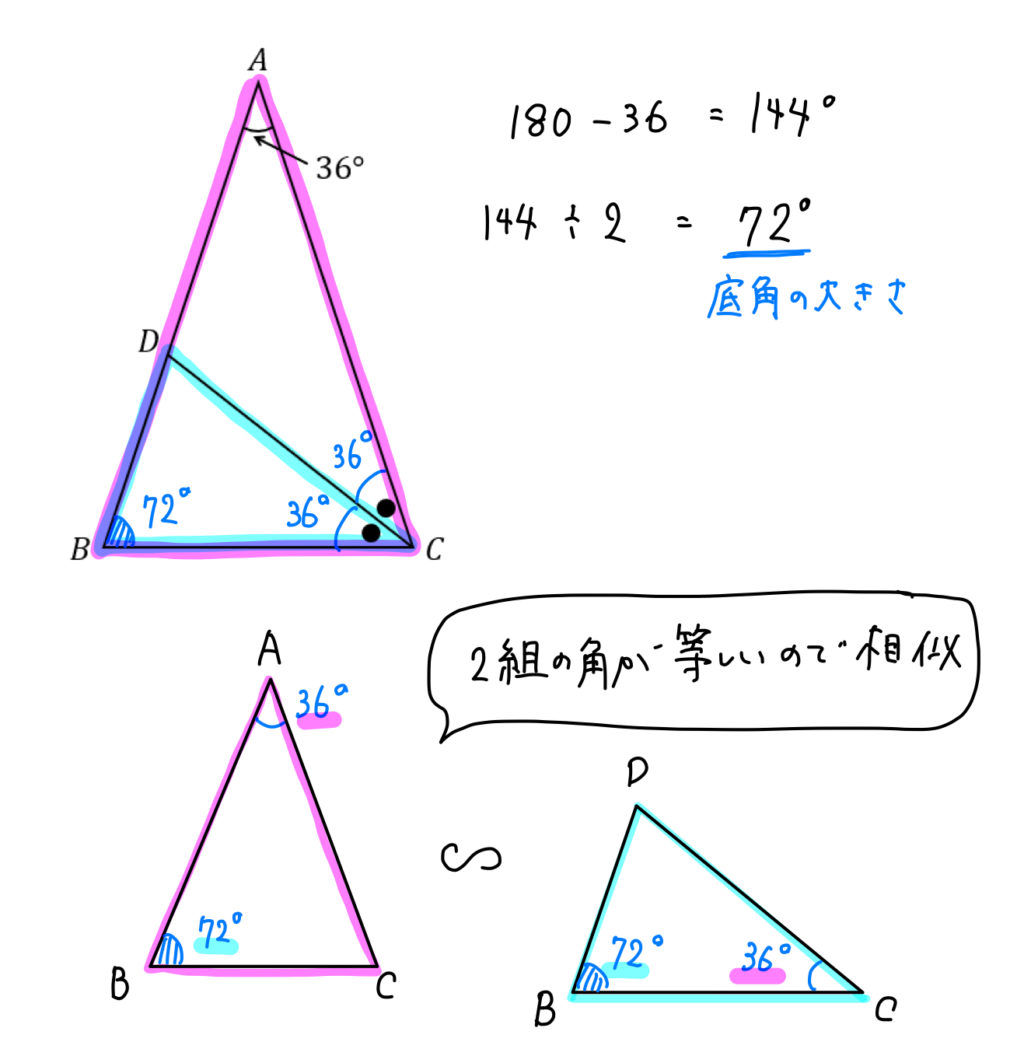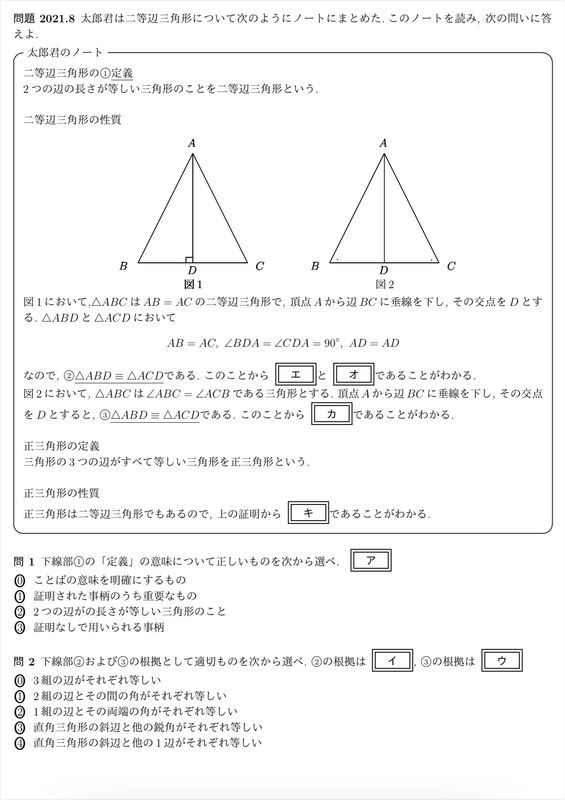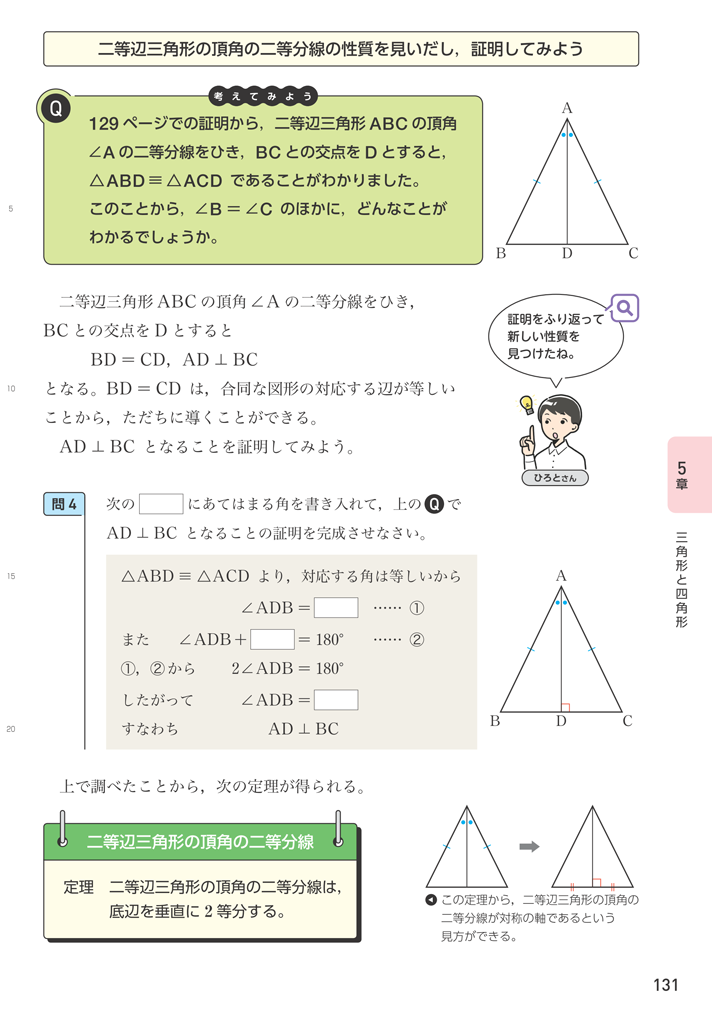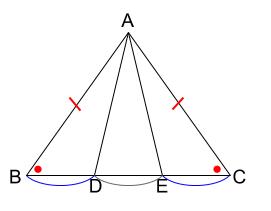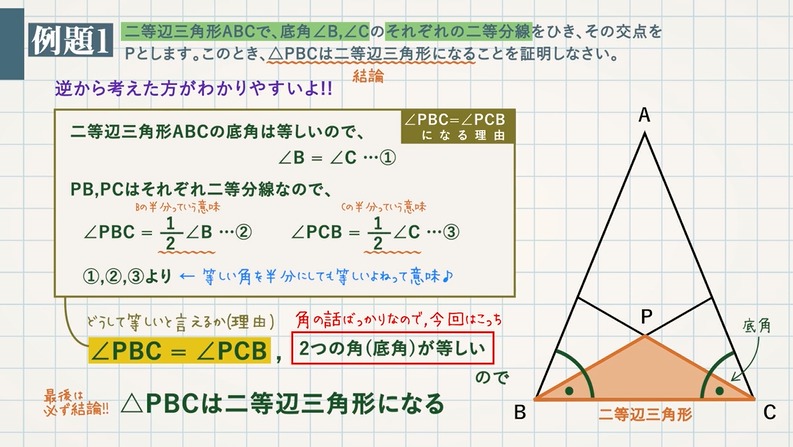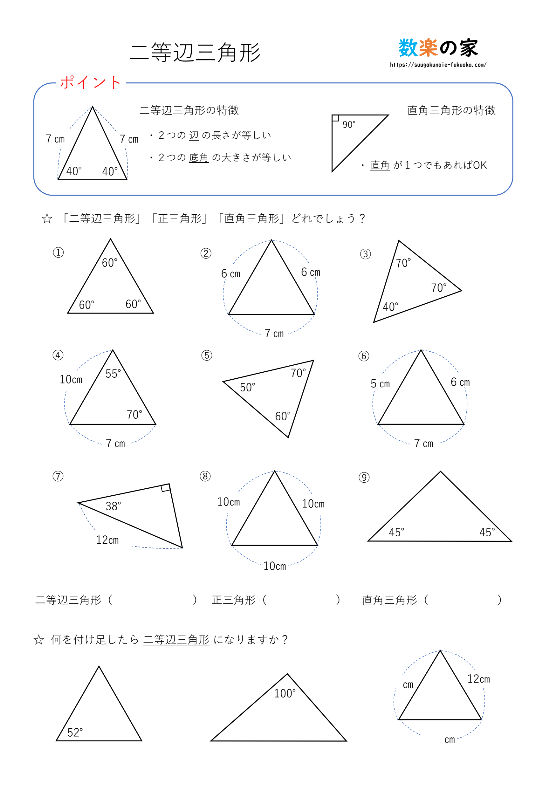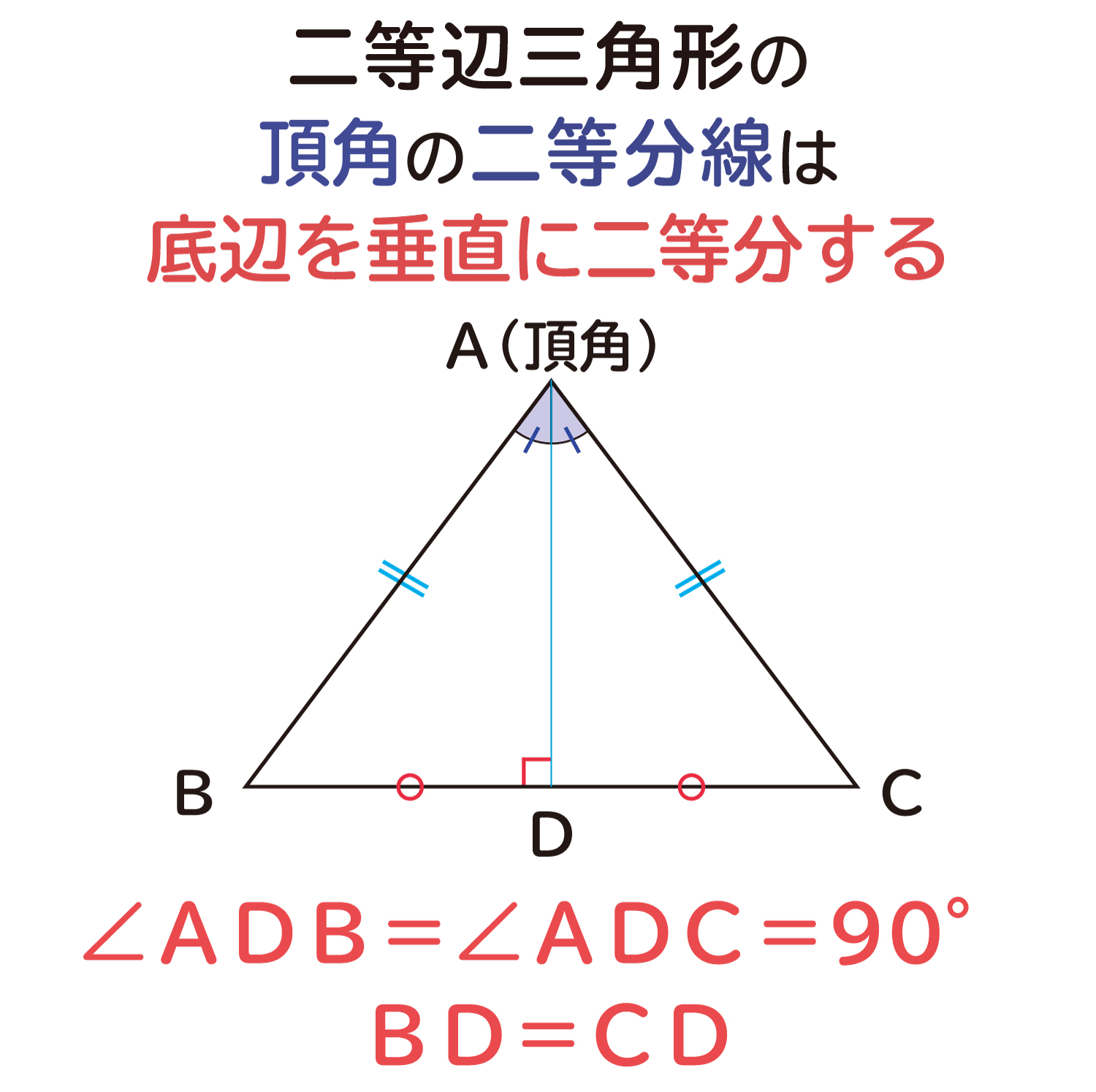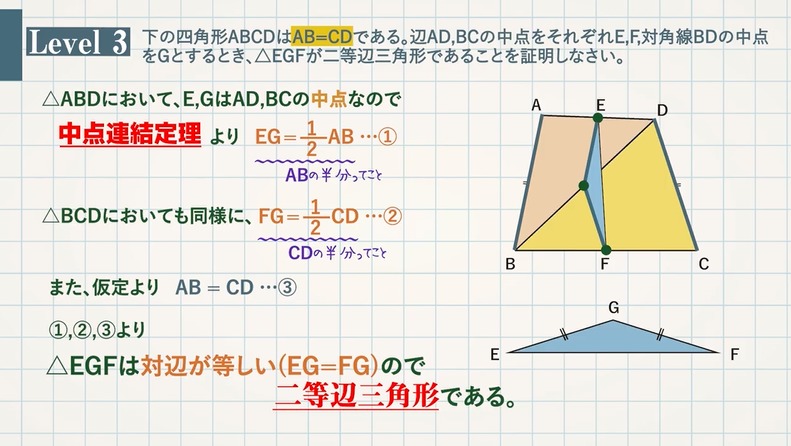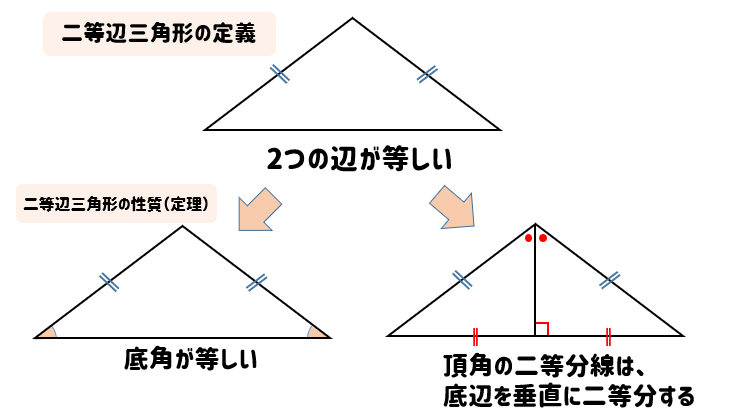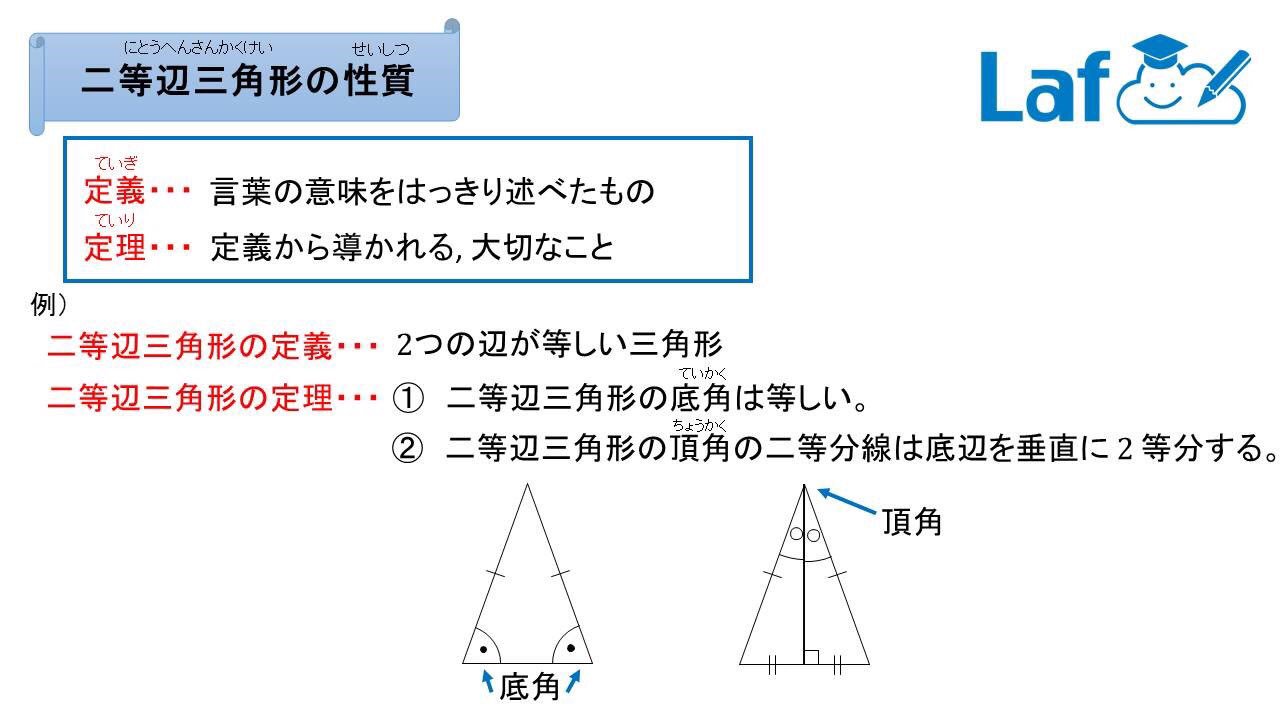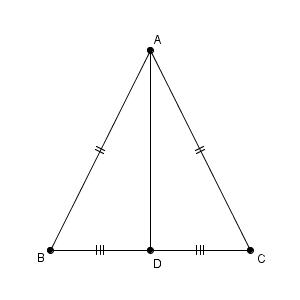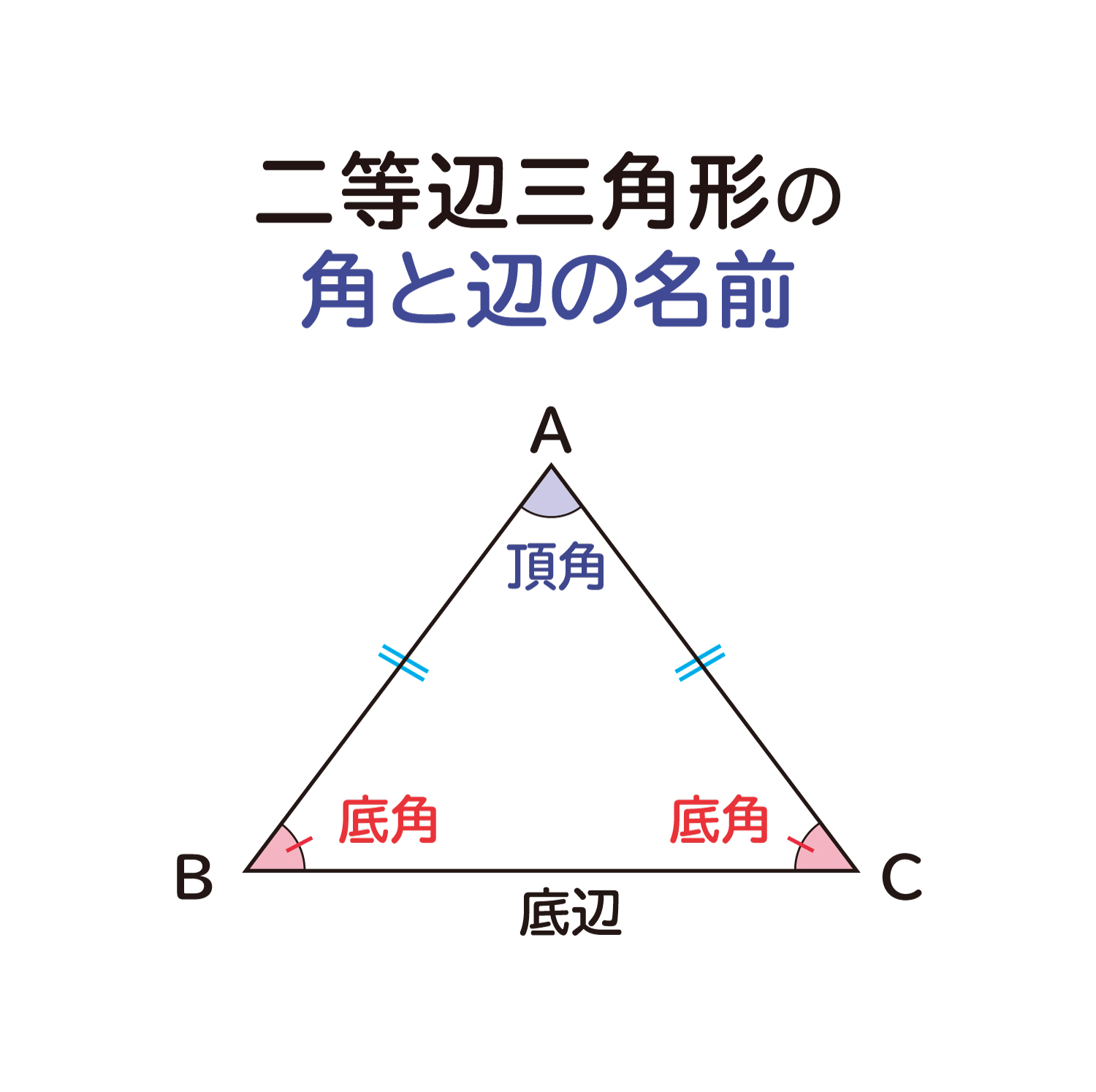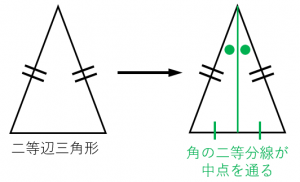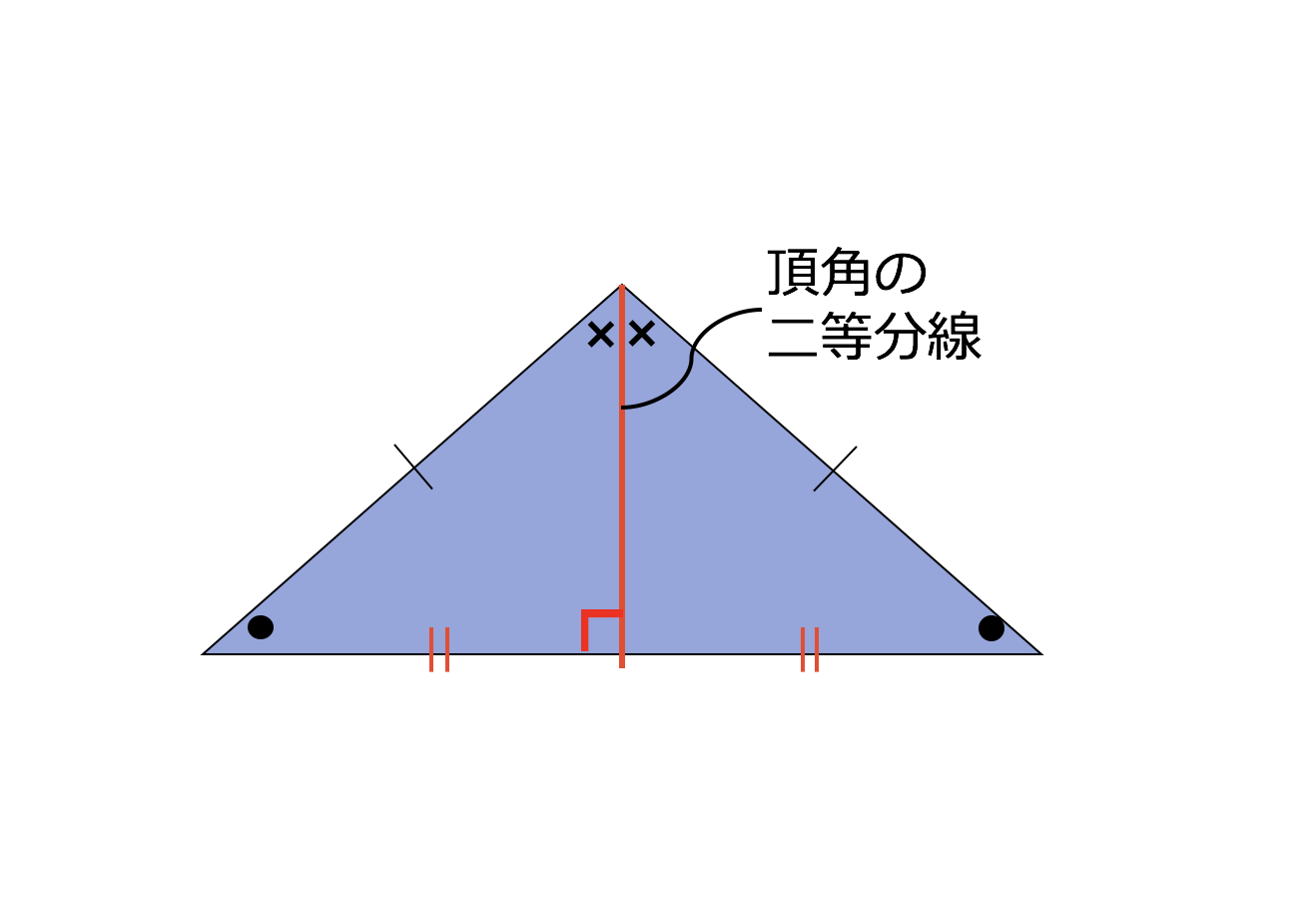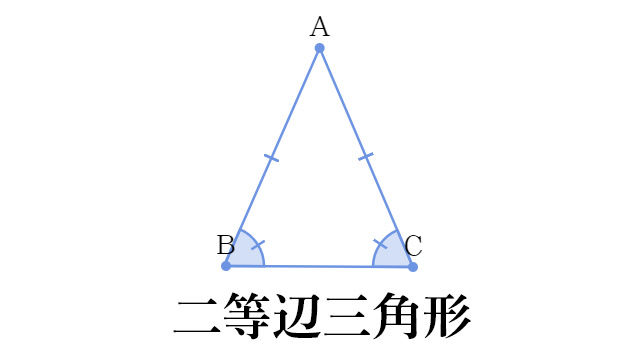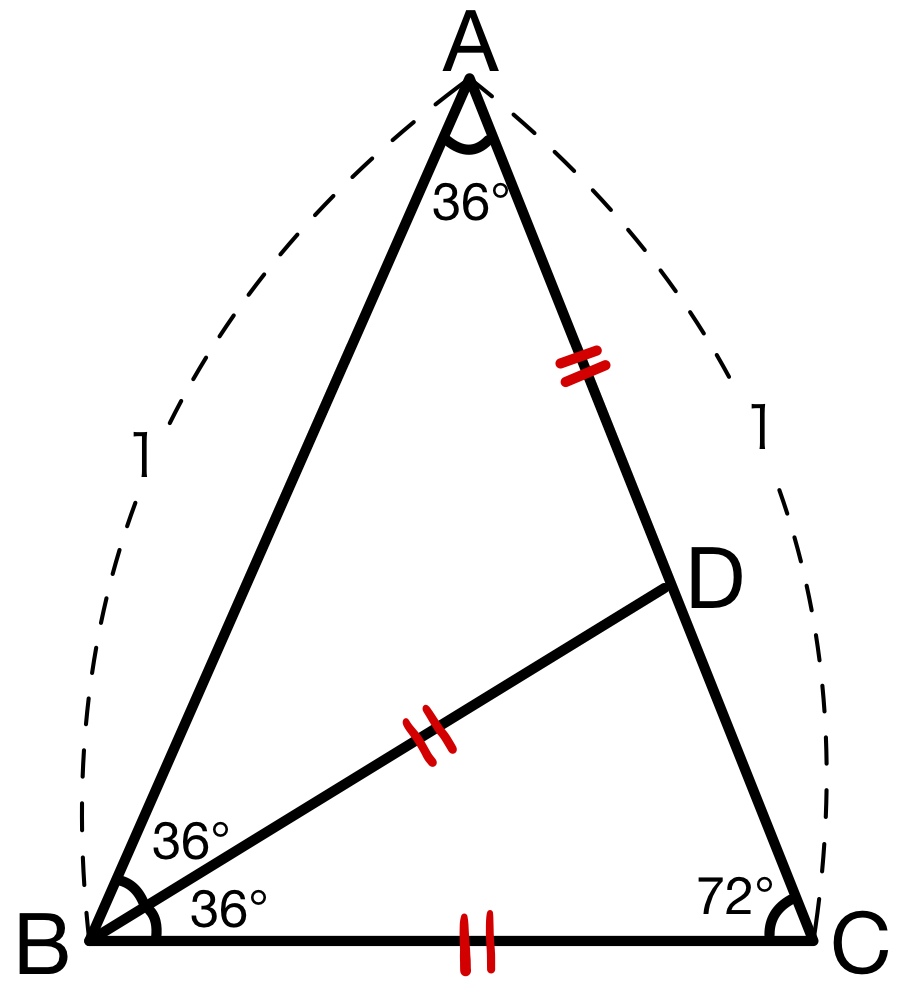 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |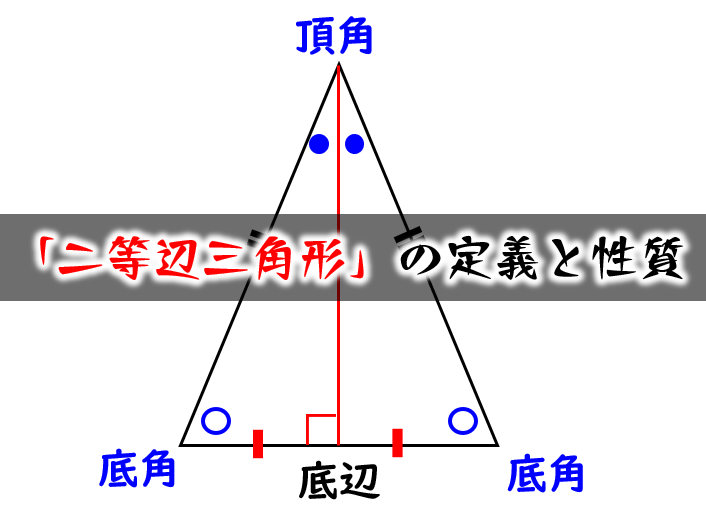
中点連結定理 Mn Mn 1 2bc 教遊者 | 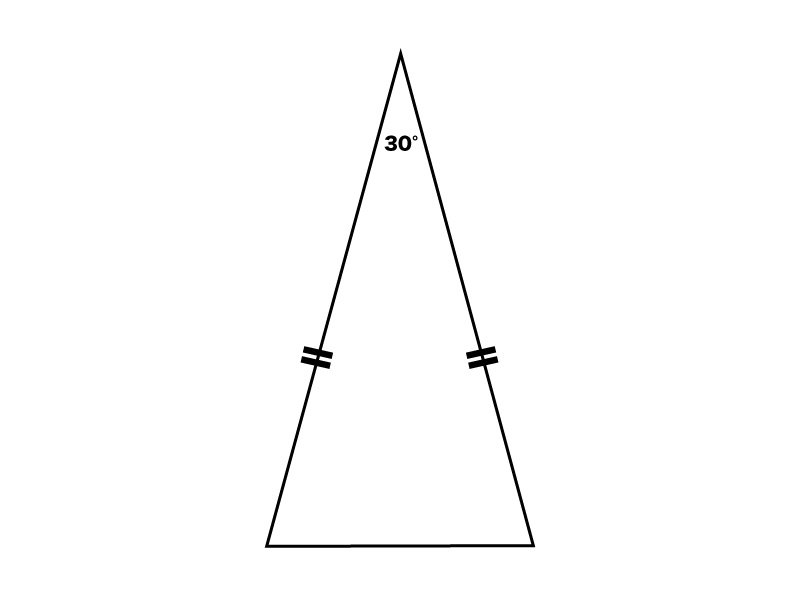 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
 中点連結定理 Mn Mn 1 2bc 教遊者 | 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
「三角形 辺の長さ 求め方 二等辺三角形」の画像ギャラリー、詳細は各画像をクリックしてください。
 中点連結定理 Mn Mn 1 2bc 教遊者 | 中点連結定理 Mn Mn 1 2bc 教遊者 | 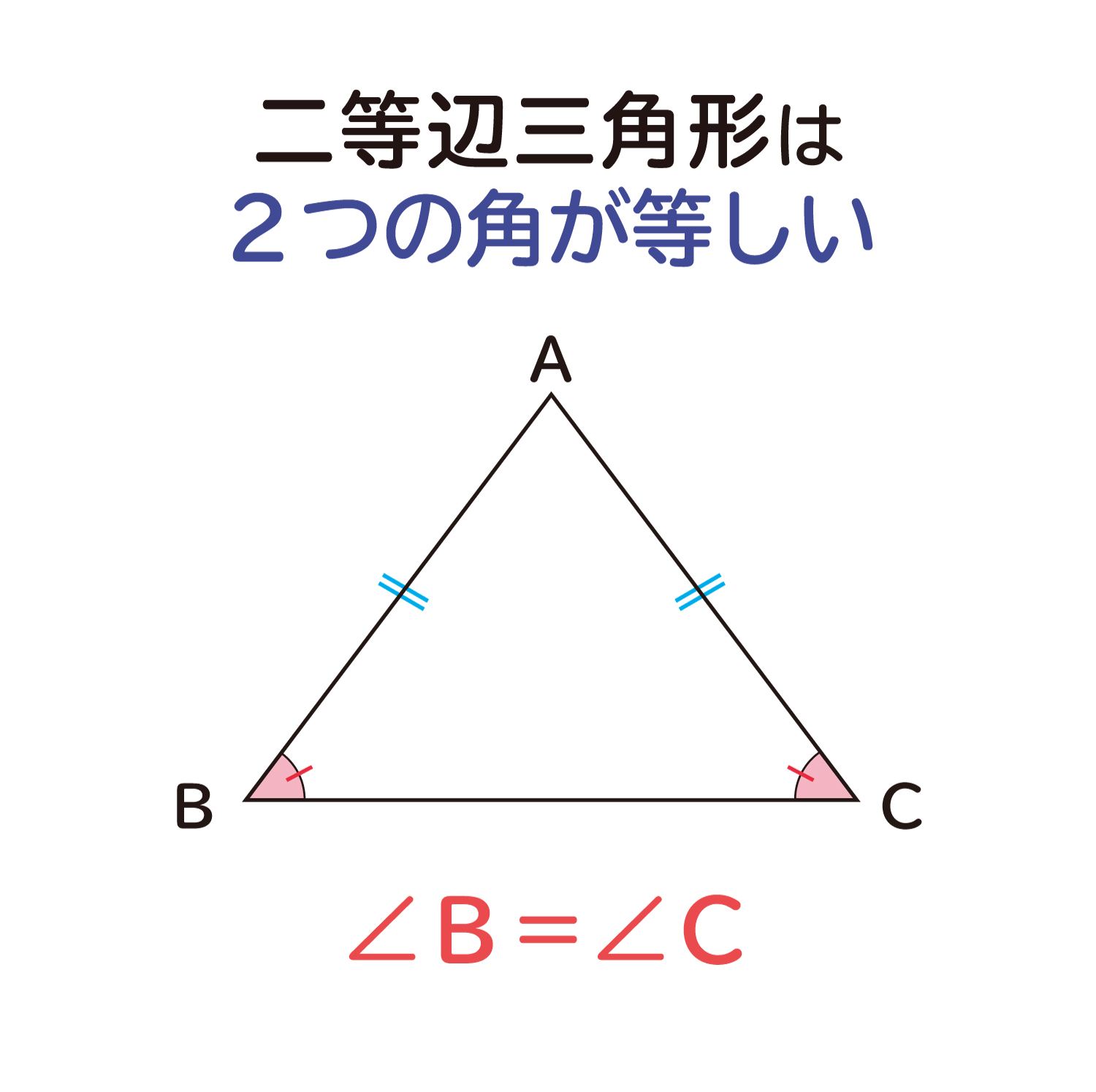 中点連結定理 Mn Mn 1 2bc 教遊者 |
 中点連結定理 Mn Mn 1 2bc 教遊者 |  中点連結定理 Mn Mn 1 2bc 教遊者 |
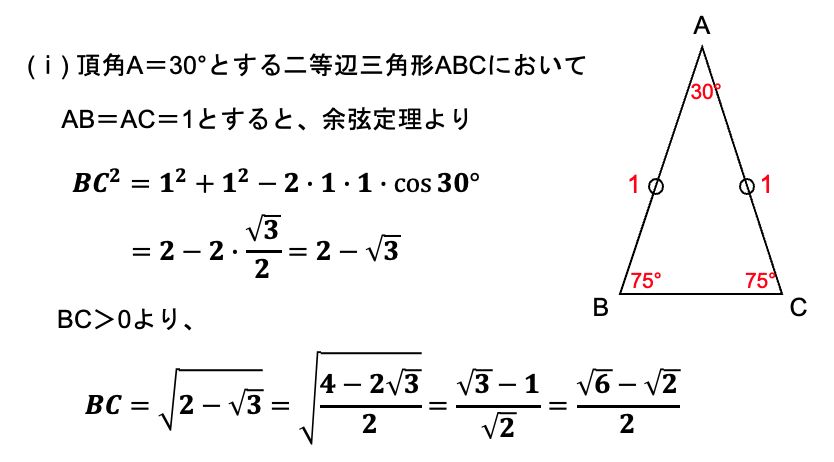
まずは、「2辺の長さとその間の角度」から「残り1辺の長さ」を求める場合。 b = A C = 4 c = A B = 6 cos A = cos 60 ° = 1 2 を代入すると、残り1辺の長さ a が求まります。 3辺の長 頂角の二等分線は底辺を垂直にニ等分する。・・・③ 二等辺三角形になるための条件 2つの角が等しい三角形は二等辺三角形である。･･･④ 二等辺三角形に関する定義と定理として
Incoming Term: 二等辺 三角形 辺の長さ 求め方, 二等辺三角形 辺の長さ 求め方 角度から, 二等辺三角形 底辺 角度 求め方, 二等辺三角形 辺の長さ 求め方 公式, 二等辺三角形 辺の長さ 求め方 角度, 三角形 辺の長さ 求め方 二等辺三角形, 数学 二等辺三角形 角度 問題, 二等辺三角形 高さ 求め方 公式, 二等辺三角形 辺の長さ 求め方 ルート, 二等辺三角形 底辺の長さ 求め方 公式, 直角二等辺三角形 辺の長さ 求め方 中学受験, 二等辺三角形 角度 問題 プリント,
0 件のコメント:
コメントを投稿